《2025年综合应用创新题典中点九年级数学下册冀教版》

1.[2024内江]下列事件中是必然事件的是( )
A.打开电视机，中央电视台正在播放“嫦娥六号完成人类首次在月背采样”的新闻
B.从两个班级中任选三名学生担任学校安全督查员，至少有两名学生来自同一个班级
C.小明在内江某平台一定能抢到龙舟节开幕式门票
D.从《西游记》《红楼梦》《三国演义》《水浒传》这四本书中随机抽取一本是《三国演义》

答案： B

2.一个不透明的盒子中有红球x个，白球10个，黑球y个，每个球除颜色外都相同，从中任取一个球，取出白球的概率与取出红球或黑球的概率相同，那么x与y的关系是( )
A.x + y = 5
B.x + y = 10
C.x = y = 5
D.x - y = 5

答案： B

3.[2024威海]如图，在扇形AOB中，∠AOB = 90°，点C是AO的中点.过点C作CE⊥AO交⌢AB于点E，过点E作ED⊥OB，垂足为点D.在扇形内随机选取一点P，则点P落在阴影部分的概率是( )
A.$\frac{1}{4}$ B.$\frac{1}{3}$ C.$\frac{1}{2}$ D.$\frac{2}{3}$
　　　

答案： B　[点拨]设扇形AOB的半径为r.
∵CE⊥AO,
∴∠OCE=90°,
∵点C是AO的中点，
∴OC=$\frac{1}{2}$OA=$\frac{1}{2}$OE.
在Rt△OCE中,
∵cos∠COE=$\frac{OC}{OE}$=$\frac{1}{2}$,
∴∠COE=60°.
∴∠BOE=∠AOB−∠COE=30°.
∵ED⊥OB,
∴∠ODE=90°.
又
∵∠COD=∠OCE=90°,
∴四边形OCED为矩形.
∴S△OCE=S△ODE.
∴阴影部分的面积=S扇形BOE.
∴点P落在阴影部分的概率=$\frac{S_{扇形BOE}}{S_{扇形AOB}}$ = $\frac{\frac{30\times\pi\times r^{2}}{360}}{\frac{90\times\pi\times r^{2}}{360}}$ = $\frac{1}{3}$.

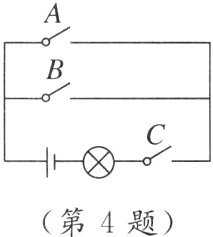
4.[新趋势 跨学科综合]如图，电路图上有3个开关A，B，C和1个小灯泡，同时闭合开关A，C或同时闭合开关B，C都可以使小灯泡发光.下列操作中，“小灯泡发光”这个事件是随机事件的是( )
A.只闭合1个开关 B.只闭合2个开关
C.闭合3个开关 D.不闭合开关
　　　

答案： B　[点拨]A.只闭合1个开关，小灯泡不会发光，小灯泡发光是不可能事件;B.只闭合2个开关，小灯泡可能发光也可能不发光，小灯泡发光是随机事件;C.闭合3个开关，小灯泡一定会发光，小灯泡发光是必然事件;D.不闭合开关，小灯泡不会发光，小灯泡发光是不可能事件.

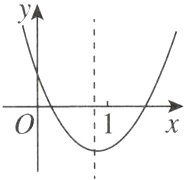
5.已知抛物线y = ax² + bx + c(a≠0)如图所示，有6张卡片，正面分别写有以下与抛物线系数有关的代数式：①ac；②abc；③2a + b；④a + b + c；⑤4a - 2b + c；⑥b² - 4ac.除正面代数式不同外，其他完全相同.将这6张卡片放在一个不透明的箱子中，从中随机取出2张，上面的代数式的值都大于0的概率是( )
A.$\frac{4}{5}$ B.$\frac{2}{5}$
C.$\frac{2}{3}$ D.$\frac{25}{36}$
　　　

答案：
B　[点拨]
∵抛物线的开口向上，
∴a＞0.
∵抛物线与y轴的交点在y轴的正半轴上,
∴c＞0.
∴ac＞0.
抛物线的对称轴为直线x= - $\frac{b}{2a}$，由图可知0＜ - $\frac{b}{2a}$＜1.
∴2a + b＞0.
∵a＞0，
∴b＜0.
∴abc＜0.
由抛物线与x轴的交点可以看出，
当x = 1时，y = a + b + c＜0，
当x = - 2时，y = 4a - 2b + c＞0.
∵抛物线与x轴有两个交点，
∴b² - 4ac＞0.
综上所述，代数式的值大于0的为①③⑤⑥，共4个，
画树形图如下:

共有30种等可能的结果，其中代数式的值都大于0的结果有12种,
∴从中随机取出2张，上面的代数式的值都大于0的概率为$\frac{12}{30}$=$\frac{2}{5}$

6.从1～10这10个整数中随机抽取1个数，抽到的数是3的倍数的概率是________.

答案： $\frac{3}{10}$

7.某射击运动员在同一条件下的射击成绩记录如下(频率保留两位小数)：
　　　　
根据频率的稳定性，估计这名运动员射击一次射中9环以上的概率是________(结果保留小数点后一位).

答案： 0.8

8.[2024上海]一个袋子中有若干个白球和绿球，它们除了颜色外都相同.随机从中摸一个球，恰好摸到绿球的概率是$\frac{3}{5}$，则袋子中至少有________个绿球.

答案： 3

9.(16分)某博物馆展厅的示意图如图①所示.嘉淇进入展厅后开始自由参观，每走到一个十字路口，她可能直行，也可能向左转或向右转，且这三种可能性均相同.
(1)求嘉淇走到道口A向北走的概率；
(2)补全图②的树形图，并分析嘉淇经过两个道口后向哪个方向参观的概率较大.
　

答案：
[解]
(1)嘉淇走到道口A向北走的概率为$\frac{1}{3}$.
(2)补全树形图如图.

共有9种等可能的结果，其中嘉淇经过两个道口后向西参观的结果有3种，向南参观的结果有2种，向北参观的结果有2种，向东参观的结果有2种,
∴向西参观的概率为$\frac{3}{9}$=$\frac{1}{3}$,向南参观的概率=向北参观的概率=向东参观的概率=$\frac{2}{9}$
∵$\frac{1}{3}$＞$\frac{2}{9}$.
∴向西参观的概率较大.