第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 情境题 生活应用 如图是记录的日出美景,图中的太阳与海天的交界处可看成圆与直线,则它们的位置关系是( )
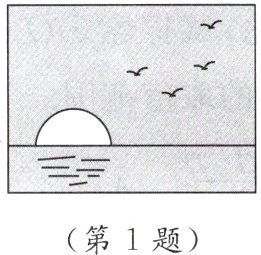
A. 相交
B. 相切
C. 相离
D. 平行

A. 相交
B. 相切
C. 相离
D. 平行
答案:
A
2. 母题 教材P7习题A组T1 如果一条直线与圆有公共点,那么该直线与圆的位置关系是( )
A. 相交
B. 相离
C. 相切
D. 相交或相切
A. 相交
B. 相离
C. 相切
D. 相交或相切
答案:
D
3. [2024承德期末] 已知⊙O的半径OE = $\sqrt{3}$,若OF = 2,则直线EF与⊙O的位置图形可能为( )


答案:
A
4. ⊙O的直径为10,直线l与⊙O相交,圆心O到l的距离为d,则下列结论正确的是( )
A. d>5
B. 0≤d<5
C. d = 5
D. d = 10
A. d>5
B. 0≤d<5
C. d = 5
D. d = 10
答案:
B
5. 已知⊙O的半径r是一元二次方程$x^{2}-2x - 3 = 0$的一个根,圆心O到直线l的距离d = 4,则直线l与⊙O的位置关系是( )
A. 相交
B. 相切
C. 相离
D. 不能确定
A. 相交
B. 相切
C. 相离
D. 不能确定
答案:
C
6. [2024邯郸期中] 如图,在矩形ABCD中,AB = 4,BC = 3,以点B为圆心,r为半径作圆,且⊙B与边CD有唯一公共点,则r的取值范围为______.
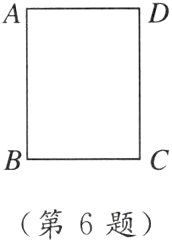

答案:
$3\leq r\leq5$
7. 如图,在△ABC中,AB = AC = 4 cm,∠BAC = 120°,以底边BC的中点D为圆心,1 cm为半径的⊙D与AB有怎样的位置关系?以点D为圆心,分别以$\sqrt{3}$cm,2 cm为半径的⊙D与AB又有怎样的位置关系?
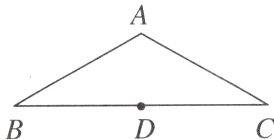

答案:
【解】如图,连接AD,作$DH\perp AB$于点H.
$\because AB = AC = 4\ cm$,$\angle BAC = 120^{\circ}$,D为BC的中点,
$\therefore AD\perp BC$,$\angle B=\angle C = 30^{\circ}$.
$\therefore$在$Rt\triangle ABD$中,易得$AD = 2\ cm$,$BD = 2\sqrt{3}\ cm$.
在$Rt\triangle BDH$中,$\angle B = 30^{\circ}$,$BD = 2\sqrt{3}\ cm$,$\therefore DH=\sqrt{3}\ cm$.
$\because 1\ cm<\sqrt{3}\ cm$,$\sqrt{3}\ cm=\sqrt{3}\ cm$,$2\ cm>\sqrt{3}\ cm$,
$\therefore$以$1\ cm$为半径的$\odot D$与AB相离,以$\sqrt{3}\ cm$为半径的$\odot D$与AB相切,以$2\ cm$为半径的$\odot D$与AB相交.

【解】如图,连接AD,作$DH\perp AB$于点H.
$\because AB = AC = 4\ cm$,$\angle BAC = 120^{\circ}$,D为BC的中点,
$\therefore AD\perp BC$,$\angle B=\angle C = 30^{\circ}$.
$\therefore$在$Rt\triangle ABD$中,易得$AD = 2\ cm$,$BD = 2\sqrt{3}\ cm$.
在$Rt\triangle BDH$中,$\angle B = 30^{\circ}$,$BD = 2\sqrt{3}\ cm$,$\therefore DH=\sqrt{3}\ cm$.
$\because 1\ cm<\sqrt{3}\ cm$,$\sqrt{3}\ cm=\sqrt{3}\ cm$,$2\ cm>\sqrt{3}\ cm$,
$\therefore$以$1\ cm$为半径的$\odot D$与AB相离,以$\sqrt{3}\ cm$为半径的$\odot D$与AB相切,以$2\ cm$为半径的$\odot D$与AB相交.

8. [2024唐山期末] 在平面直角坐标系xOy中,以点A(1,3)为圆心,2为半径作⊙A,下列判断正确的是( )
A. ⊙A与x轴相交
B. ⊙A与y轴相切
C. 点O在⊙A外
D. 点(1,1)在⊙A内
A. ⊙A与x轴相交
B. ⊙A与y轴相切
C. 点O在⊙A外
D. 点(1,1)在⊙A内
答案:
C
9. [2024上海虹口区模拟] 在□ABCD中,BC = 5,$S_{□ABCD}=20$. 如果以顶点C为圆心,BC长为半径作⊙C,那么⊙C与边AD所在直线的公共点的个数是( )
A. 3
B. 2
C. 1
D. 0
A. 3
B. 2
C. 1
D. 0
答案:
B 【点拨】作$CH\perp DA$所在直线于点H.
$\because S_{\square ABCD}=BC\cdot CH = 20$,$\therefore CH=\frac{20}{BC}=\frac{20}{5}=4$.
$\because 4<5$,$\therefore$直线AD与$\odot C$相交,
$\therefore\odot C$与直线AD有2个公共点,故选B.
$\because S_{\square ABCD}=BC\cdot CH = 20$,$\therefore CH=\frac{20}{BC}=\frac{20}{5}=4$.
$\because 4<5$,$\therefore$直线AD与$\odot C$相交,
$\therefore\odot C$与直线AD有2个公共点,故选B.
10. 易错题 在直角坐标系中,以点P(1,2)为圆心,r为半径画圆,与坐标轴恰好有三个交点,则r应满足( )
A. r = 2或$\sqrt{5}$
B. r = 2
C. r = $\sqrt{5}$
D. 2≤r≤$\sqrt{5}$
A. r = 2或$\sqrt{5}$
B. r = 2
C. r = $\sqrt{5}$
D. 2≤r≤$\sqrt{5}$
答案:
A 【点拨】$\because$以点$P(1,2)$为圆心,$r$为半径画圆,与坐标轴恰好有三个交点,$\therefore\odot P$与$x$轴相切(如图①)或$\odot P$过原点(如图②). 当$\odot P$与$x$轴相切时,$r = 2$;当$\odot P$过原点时,连接OP,$r = OP=\sqrt{1^{2}+2^{2}}=\sqrt{5}$. $\therefore r = 2$或$\sqrt{5}$.
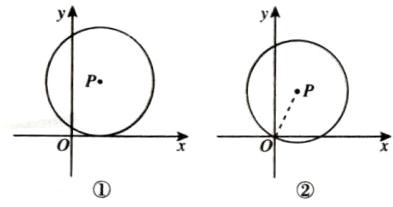
△点易错 本题中$\odot P$与坐标轴恰好有三个交点,可以分为两种情况:$\odot P$与$x$轴相切或$\odot P$过原点,不要漏掉过原点这一种情况.
A 【点拨】$\because$以点$P(1,2)$为圆心,$r$为半径画圆,与坐标轴恰好有三个交点,$\therefore\odot P$与$x$轴相切(如图①)或$\odot P$过原点(如图②). 当$\odot P$与$x$轴相切时,$r = 2$;当$\odot P$过原点时,连接OP,$r = OP=\sqrt{1^{2}+2^{2}}=\sqrt{5}$. $\therefore r = 2$或$\sqrt{5}$.

△点易错 本题中$\odot P$与坐标轴恰好有三个交点,可以分为两种情况:$\odot P$与$x$轴相切或$\odot P$过原点,不要漏掉过原点这一种情况.
11. 如图,在直线l上有相距12 cm的两点A和O(点A在点O的右侧),以O为圆心作半径为2 cm的圆,过点A作直线AB⊥l. 将⊙O以2 cm/s的速度向右移动(点O始终在直线l上),则经过______s,⊙O与直线AB相切.


答案:
5或7 【点拨】设经过$t\ s$,$\odot O$与直线AB相切. 当点C到AB的距离为$2\ cm$时,$\odot O$与AB相切,$\because$开始时点C到AB的距离为$12\ cm$,
$\therefore$当圆向右移动$12 - 2 = 10(cm)$或$12 + 2 = 14(cm)$时,点O到AB的距离为$2\ cm$.
$\therefore t = 10\div2 = 5$或$t = 14\div2 = 7$.
$\therefore$经过$5\ s$或$7\ s$,$\odot O$与直线AB相切.
$\therefore$当圆向右移动$12 - 2 = 10(cm)$或$12 + 2 = 14(cm)$时,点O到AB的距离为$2\ cm$.
$\therefore t = 10\div2 = 5$或$t = 14\div2 = 7$.
$\therefore$经过$5\ s$或$7\ s$,$\odot O$与直线AB相切.
查看更多完整答案,请扫码查看


