《2025年综合应用创新题典中点九年级数学下册冀教版》

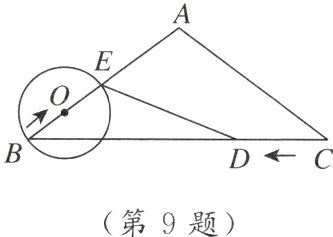
9. 新视角 动点探究题 如图，在等腰三角形ABC中，AB=AC=5 cm，BC=8 cm. 动点D从点C出发，沿线段CB以2 cm/s的速度向点B运动，同时动点O从点B出发，沿线段BA以1 cm/s的速度向点A运动，当其中一个动点停止运动时，另一个动点也随之停止. 设运动时间为t s，以点O为圆心，OB长为半径的⊙O与BA交于另一点E，连接ED. 当直线DE与⊙O相切时，t的值是_______.

答案：
$\frac{16}{9}$ [点拨]如图,作AH⊥BC于点H,则∠BHA=90°.
由题意得BE=2tcm,BD=(8−2t)cm.
∵AB=AC,BC=8cm,AH⊥BC,
∴BH=CH=$\frac{1}{2}$BC=4cm.

当直线DE与⊙O相切时，BE⊥DE,则∠BED=90°,
∵∠EBD=∠ABH,∠BED=∠BHA=90°,
∴△BED∽△BHA,
∴$\frac{BE}{BH}$=$\frac{BD}{BA}$,即$\frac{2t}{4}$=$\frac{8−2t}{5}$,解得t=$\frac{16}{9}$,即t的值是$\frac{16}{9}$.

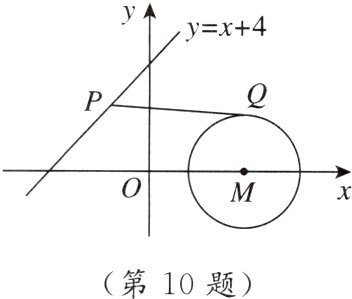
10. 如图，⊙M的圆心为M(4，0)，半径为2，P是直线y=x+4上的一个动点，过点P作⊙M的切线，切点为Q，则PQ的最小值为_______.

答案：
2$\sqrt{7}$ [点拨]如图,连接MP,MQ,设直线y=x+4与x轴、y轴分别交于点A,B.
∵PQ是⊙M的切线，

∴MQ⊥PQ.
∴在Rt△MQP中,PQ=$\sqrt{PM^{2}-MQ^{2}}$=$\sqrt{PM^{2}-4}$
∴当PM最小时，PQ最小.
当MP⊥AB时，PM最小.
易得直线y=x+4与x轴的交点A的坐标为(−4,0),与y轴的交点B的坐标为(0,4),
∴OA=OB=4,AM=8.
∴∠BAO=45°.
当MP⊥AB时,PM=AM·sin∠BAO=8×$\frac{\sqrt{2}}{2}$=4$\sqrt{2}$
∴PQ的最小值为$\sqrt{(4\sqrt{2})^{2}-4}$=2$\sqrt{7}$.

11. [2024邯郸模拟] 如图，A为⊙O外一点，线段AC交⊙O于点B，C，AB=10，BC=8，⊙O的半径为5，点P为⊙O上一动点.
（1）当△APC的面积最大时，求PC的长；
（2）当AP与⊙O相切时，求AP的长.

答案：
[解]
(1)如图①,作OQ⊥AC于点Q,延长QO交⊙O于点P,连接OC,OP,易知当Q,O,P三点共线时，△APC的面积最大，
∵OQ⊥AC,
∴CQ=BQ=$\frac{1}{2}$BC=4.
∴OQ=$\sqrt{OC^{2}-CQ^{2}}$=$\sqrt{5^{2}-4^{2}}$=3.
∴PQ=OP+OQ=5+3=8.
∴PC=$\sqrt{CQ^{2}+PQ^{2}}$=$\sqrt{4^{2}+8^{2}}$=4$\sqrt{5}$.

(2)如图②,当AP与⊙O相切时,作直径PD,连接BD,BP,则∠PBD=90°.
∴∠D + ∠BPD = 90°.
∵$\overset{\frown}{BP}=\overset{\frown}{BP}$，
∴∠C = ∠D.
∴∠C + ∠BPD = 90°.
∵AP是⊙O的切线，
∴PD⊥AP.
∴∠APD = 90°.
∴∠APB + ∠BPD = 90°,
∴∠APB = ∠C;
又
∵∠A = ∠A,
∴△APB∽△ACP.
∴$\frac{AP}{AC}$=$\frac{AB}{AP}$.即$\frac{AP}{10 + 8}$=$\frac{10}{AP}$.
∴AP = 6$\sqrt{5}$(负值已舍去).

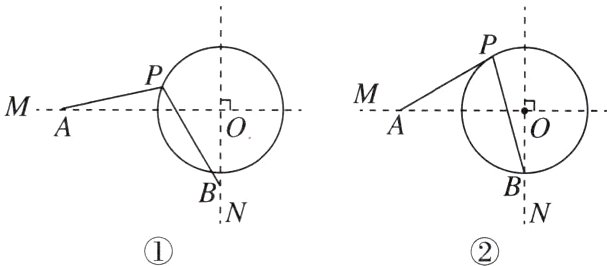
12. 新考向 传统文化 在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”. 小明受此启发设计了一个“双连杆机构”，设计图如图①，两个固定长度的“连杆”AP，BP的连接点P在⊙O上，当点P在⊙O上转动时，带动点A，B分别在射线OM，ON上滑动，OM⊥ON. 当AP与⊙O相切时，点B恰好落在⊙O上，如图②. 请仅就图②的情形解答下列问题：
（1）求证：∠PAO=2∠PBO；
（2）若⊙O的半径为3，AP=4，求BP的长.

答案：

(1)[证明]如图，连接OP,设直线ON与圆的另一交点为Q.
∵AP与⊙O相切，
∴OP⊥AP.
∴∠APO = 90°.
∴∠PAO + ∠POA = 90°.
∵OM⊥ON，
∴∠AOQ = 90°.
∴∠POQ + ∠POA = 90°.
∴∠POQ = ∠PAO.
∵点B恰好落在⊙O上，
∴∠PBO = $\frac{1}{2}$∠POQ = $\frac{1}{2}$∠PAO.
∴∠PAO = 2∠PBO.

(2)[解]如图,过点P作PD⊥BQ于点D,则∠PDO = 90°,由
(1)可知∠POQ = ∠PAO,∠APO = 90°,
∴∠PDO = ∠APO.
∴△PDO∽△OPA.
∴$\frac{PD}{OP}=\frac{OD}{AP}=\frac{OP}{AO}$.
∵⊙O的半径为3,AP = 4,
∴AO = $\sqrt{AP^{2}+OP^{2}}$ = 5.
∴$\frac{PD}{3}=\frac{OD}{4}=\frac{3}{5}$
∴PD = $\frac{9}{5}$,OD = $\frac{12}{5}$.
∴BD = OB + OD = 3 + $\frac{12}{5}$ = $\frac{27}{5}$.
∴在Rt△PBD中,PB = $\sqrt{PD^{2}+BD^{2}}$ = $\sqrt{(\frac{9}{5})^{2}+(\frac{27}{5})^{2}}$ = $\frac{9\sqrt{10}}{5}$