第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
10. 如图,正方形四个顶点的坐标依次为 $(1,-1)$,$(3,-1)$,$(3,-3)$,$(1,-3)$,若抛物线 $y = ax^{2}$ 与正方形的边有公共点,则实数 $a$ 的取值范围是__________.


答案:
$-3≤a≤-\frac{1}{9} [$点拨]
∵抛物线的表达式为y=ax²,
∴当抛物线经过(1,-3)时,a=-3,当抛物线经过(3,-1)时,$a=-\frac{1}{9}.$
∴a的取值范围是$-3≤a≤-\frac{1}{9}.$
∵抛物线的表达式为y=ax²,
∴当抛物线经过(1,-3)时,a=-3,当抛物线经过(3,-1)时,$a=-\frac{1}{9}.$
∴a的取值范围是$-3≤a≤-\frac{1}{9}.$
11. (12分)已知抛物线 $y = a(x + 4)^{2}+4(a\neq0)$ 经过点 $(2,-2)$.
(1)$a$ 的值为________;
(2)若点 $A(x_{1},y_{1})$,$B(x_{2},y_{2})(x_{1}\lt x_{2}\lt - 4)$ 都在该抛物线上,试比较 $y_{1}$ 与 $y_{2}$ 的大小.
(1)$a$ 的值为________;
(2)若点 $A(x_{1},y_{1})$,$B(x_{2},y_{2})(x_{1}\lt x_{2}\lt - 4)$ 都在该抛物线上,试比较 $y_{1}$ 与 $y_{2}$ 的大小.
答案:
[解$](1)-\frac{1}{6} [$点拨]
∵抛物线y=a(x+4)²+4(a≠0)过点(2,-2),
∴-2=a(2+4)²+4,解得$a=-\frac{1}{6}.(2)$由
(1)可知抛物线的开口向下,
∴在对称轴左侧,y随x的增大而增大.易知其对称轴为直线x=-4.
∵x₁<x₂<-4,
∴y₁<y₂.
∵抛物线y=a(x+4)²+4(a≠0)过点(2,-2),
∴-2=a(2+4)²+4,解得$a=-\frac{1}{6}.(2)$由
(1)可知抛物线的开口向下,
∴在对称轴左侧,y随x的增大而增大.易知其对称轴为直线x=-4.
∵x₁<x₂<-4,
∴y₁<y₂.
12. (14分)[2024廊坊校级月考] 已知抛物线 $y=-x^{2}+c$ 经过点 $(-2,a)$ 和点 $(2,b)$.
(1)写出该抛物线的对称轴,并直接写出 $a$,$b$ 的大小关系.
(2)若该抛物线经过点 $A(3,-5)$.
①$c =$________;
②当 $-1\lt x\lt2$ 时,求 $y$ 的取值范围;
③若抛物线先向下平移4个单位长度,再向右平移 $m(m\gt0)$ 个单位长度后再次经过点 $A$,请直接写出 $m$ 的值.
(1)写出该抛物线的对称轴,并直接写出 $a$,$b$ 的大小关系.
(2)若该抛物线经过点 $A(3,-5)$.
①$c =$________;
②当 $-1\lt x\lt2$ 时,求 $y$ 的取值范围;
③若抛物线先向下平移4个单位长度,再向右平移 $m(m\gt0)$ 个单位长度后再次经过点 $A$,请直接写出 $m$ 的值.
答案:
[解]
(1)该抛物线的对称轴是y轴.
a=b.
(2)①4
②由①知,抛物线的表达式为y=-x²+4,
当x=0时,y=4,
当x=2时,y=-4+4=0,
∴当-1<x<2时,$0<y≤4.③m=3+\sqrt{5}$或$m=3-\sqrt{5}. [$点拨]将抛物线先向下平移4个单位长度,再向右平移m(m>0)个单位长度后得到抛物线y=-(x-m)²+4-4,即y=-(x-m)².
∵平移后的抛物线经过点A,
∴-5=-(3-m)²,解得$m=3+\sqrt{5}$或$m=3-\sqrt{5}.$
(1)该抛物线的对称轴是y轴.
a=b.
(2)①4
②由①知,抛物线的表达式为y=-x²+4,
当x=0时,y=4,
当x=2时,y=-4+4=0,
∴当-1<x<2时,$0<y≤4.③m=3+\sqrt{5}$或$m=3-\sqrt{5}. [$点拨]将抛物线先向下平移4个单位长度,再向右平移m(m>0)个单位长度后得到抛物线y=-(x-m)²+4-4,即y=-(x-m)².
∵平移后的抛物线经过点A,
∴-5=-(3-m)²,解得$m=3+\sqrt{5}$或$m=3-\sqrt{5}.$
13. (20分) 新视角 新定义型题 如图,在平面直角坐标系中,点 $P$ 从原点 $O$ 出发,沿 $x$ 轴向右以每秒1个单位长度的速度运动 $t(t\gt0)$ 秒,抛物线 $y = x^{2}+bx + c$ 经过点 $O$ 和点 $P$. 已知矩形 $ABCD$ 的三个顶点分别为 $A(1,0)$,$B(1,-5)$,$D(4,0)$.
(1)求 $c$,$b$(用含 $t$ 的代数式表示).
(2)嘉琪认为:当这条抛物线经过点 $B$ 时,一定不会经过点 $C$. 请你通过计算说明他的说法是否正确.
(3)当 $1\lt t\lt6$ 时,设抛物线与线段 $AB$ 交于点 $M$. 在点 $P$ 的运动过程中,你认为 $\angle AMP$ 的大小是否会变化?若变化,说明理由;若不变,求出 $\angle AMP$ 的度数.
(4)在矩形 $ABCD$ 的内部(不含边界),把横、纵坐标都是整数的点称为“好点”. 若抛物线将这些“好点”分成数量相等的两部分,请直接写出 $t$ 的取值范围.
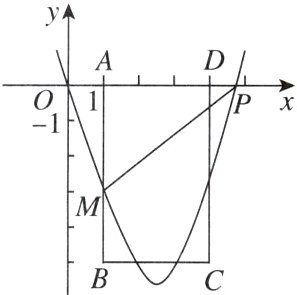
(1)求 $c$,$b$(用含 $t$ 的代数式表示).
(2)嘉琪认为:当这条抛物线经过点 $B$ 时,一定不会经过点 $C$. 请你通过计算说明他的说法是否正确.
(3)当 $1\lt t\lt6$ 时,设抛物线与线段 $AB$ 交于点 $M$. 在点 $P$ 的运动过程中,你认为 $\angle AMP$ 的大小是否会变化?若变化,说明理由;若不变,求出 $\angle AMP$ 的度数.
(4)在矩形 $ABCD$ 的内部(不含边界),把横、纵坐标都是整数的点称为“好点”. 若抛物线将这些“好点”分成数量相等的两部分,请直接写出 $t$ 的取值范围.

答案:
[解]
(1)由题意得OP=t(t>0),
∴P(t,0).
∵y=x²+bx+c经过点O和点P,
∴$\begin{cases}0+0+c=0,$$\\t²+bt+c=0.\end{cases}$解得$\begin{cases}c=0,$$\\b=-t.\end{cases}(2)$嘉琪的说法正确,理由如下:
∵矩形ABCD的三个顶点分别为A(1,0),B(1,-5),D(4,0),
∴C(4,-5).
由
(1)得y=x²-tx,把B(1,-5)代入,得1-t=-5,解得t=6,
∴当抛物线经过点B时,抛物线的表达式为y=x²-6x.当x=4时,y=16-24=-8≠-5,
∴点C不在抛物线上.
∴嘉琪的说法正确.
(3)不变.在点P运动的过程中,OP=t,
∵A(1,0),1<t<6,
∴AP=t-1.
∵抛物线y=x²-tx与线段AB交于点M,
∴M(1,1-t).
∴AM=t-1.
∴AM=AP.
在矩形ABCD中,∠BAD=90°,
∴tan∠AMP=\frac{AP}{AM}=1.
∴∠AMP=45°.
(4)\frac{7}{2}<t<\frac{11}{3}. [点拨]在矩形ABCD中共有8个“好点”.
Ⅰ.若左边4个“好点”在抛物线上方,右边4个“好点”在抛物线下方,则当x=2时,y<-4,x=3时,y>-1,
即$\begin{cases}4-2t$<-4,\\9-3t>-1,$\end{cases}$解得$\begin{cases}t>4,$$\\t$<\frac{10}{3},\end{cases}
∴此时无解.
Ⅱ.若左边3个“好点”在抛物线上方,右边3个“好点”在抛物线下方,则当x=2时,-4<y<-3,当x=3时,-2<y<-1,即-4<4-2t<-3,-2<9-3t<-1,
∴\frac{7}{2}<t<4且\frac{10}{3}<t<\frac{11}{3}.
∴\frac{7}{2}<t<\frac{11}{3}.
Ⅲ.若左边2个“好点”在抛物线上方,右边2个“好点”在抛物线下方,则当x=2时,-3<y<-2,当x=3时,-3<y<-2,即-3<4-2t<-2,-3<9-3t<-2,此时无解.
Ⅳ.若左边1个“好点”在抛物线上方,右边1个“好点”在抛物线下方,则当x=2时,-2<y<-1,当x=3时,-4<y<-3,即-2<4-2t<-1,-4<9-3t<-3,此时无解.
Ⅴ.若左边0个“好点”在抛物线上方,右边0个“好点”在抛物线下方,则当x=2时,y>-1,当x=3时,y<-4,即4-2t>-1,9-3t<-4,此时无解.
综上,t的取值范围是$\frac{7}{2}<t<\frac{11}{3}.$
(1)由题意得OP=t(t>0),
∴P(t,0).
∵y=x²+bx+c经过点O和点P,
∴$\begin{cases}0+0+c=0,$$\\t²+bt+c=0.\end{cases}$解得$\begin{cases}c=0,$$\\b=-t.\end{cases}(2)$嘉琪的说法正确,理由如下:
∵矩形ABCD的三个顶点分别为A(1,0),B(1,-5),D(4,0),
∴C(4,-5).
由
(1)得y=x²-tx,把B(1,-5)代入,得1-t=-5,解得t=6,
∴当抛物线经过点B时,抛物线的表达式为y=x²-6x.当x=4时,y=16-24=-8≠-5,
∴点C不在抛物线上.
∴嘉琪的说法正确.
(3)不变.在点P运动的过程中,OP=t,
∵A(1,0),1<t<6,
∴AP=t-1.
∵抛物线y=x²-tx与线段AB交于点M,
∴M(1,1-t).
∴AM=t-1.
∴AM=AP.
在矩形ABCD中,∠BAD=90°,
∴tan∠AMP=\frac{AP}{AM}=1.
∴∠AMP=45°.
(4)\frac{7}{2}<t<\frac{11}{3}. [点拨]在矩形ABCD中共有8个“好点”.
Ⅰ.若左边4个“好点”在抛物线上方,右边4个“好点”在抛物线下方,则当x=2时,y<-4,x=3时,y>-1,
即$\begin{cases}4-2t$<-4,\\9-3t>-1,$\end{cases}$解得$\begin{cases}t>4,$$\\t$<\frac{10}{3},\end{cases}
∴此时无解.
Ⅱ.若左边3个“好点”在抛物线上方,右边3个“好点”在抛物线下方,则当x=2时,-4<y<-3,当x=3时,-2<y<-1,即-4<4-2t<-3,-2<9-3t<-1,
∴\frac{7}{2}<t<4且\frac{10}{3}<t<\frac{11}{3}.
∴\frac{7}{2}<t<\frac{11}{3}.
Ⅲ.若左边2个“好点”在抛物线上方,右边2个“好点”在抛物线下方,则当x=2时,-3<y<-2,当x=3时,-3<y<-2,即-3<4-2t<-2,-3<9-3t<-2,此时无解.
Ⅳ.若左边1个“好点”在抛物线上方,右边1个“好点”在抛物线下方,则当x=2时,-2<y<-1,当x=3时,-4<y<-3,即-2<4-2t<-1,-4<9-3t<-3,此时无解.
Ⅴ.若左边0个“好点”在抛物线上方,右边0个“好点”在抛物线下方,则当x=2时,y>-1,当x=3时,y<-4,即4-2t>-1,9-3t<-4,此时无解.
综上,t的取值范围是$\frac{7}{2}<t<\frac{11}{3}.$
查看更多完整答案,请扫码查看


