《2025年综合应用创新题典中点九年级数学下册冀教版》

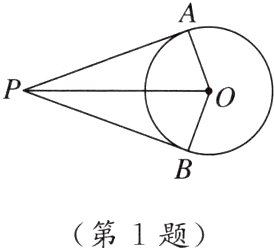
1. 如图，PA，PB是⊙O的切线，切点分别为A，B，连接OA，OB，OP，∠APB = 40°，下列结论不正确的是（ ）
A. PA = PB
B. ∠APO = 20°
C. ∠OBP = 70°
D. ∠AOP = 70°
　　

答案： C

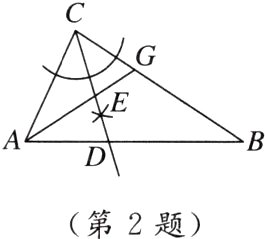
2. 如图，在△ABC中，AG平分∠CAB，使用尺规作射线CD，与AG交于点E，下列判断正确的是（ ）
A. AG平分CD
B. ∠AED = ∠ADE
C. 点E是△ABC的内心
D. 点E到点A，B，C的距离相等
　　

答案： C

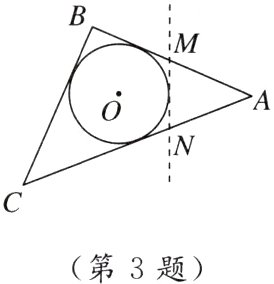
3. 母题 教材P12例1 如图，△ABC是一张周长为17 cm的三角形纸片，BC = 5 cm，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的△AMN的周长为（ ）
A. 12 cm
B. 7 cm
C. 6 cm
D. 随直线MN位置的变化而变化
　　

答案： B

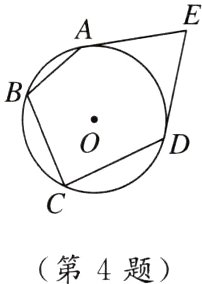
4. [2024泸州] 如图，EA，ED是⊙O的切线，切点分别为A，D，点B，C在⊙O上，若∠BAE + ∠BCD = 236°，则∠E =（ ）
A. 56°
B. 60°
C. 68°
D. 70°
　　

答案： C　[点拨]连接AD.
∵四边形ABCD是⊙O的内接四边形，
∴∠BAD+∠BCD=180°.
∵∠BAE+∠BCD=236°,
∴∠EAD+∠BAD+∠BCD=∠EAD+180°=236°.
∴∠EAD=56°.
∵EA,ED是⊙O的切线,切点分别为A,D,
∴EA=ED.
∴∠EDA=∠EAD=56°.
∴∠E=180°−∠EDA−∠EAD=180°−56°−56°=68°.

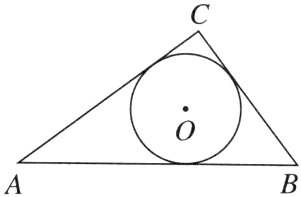
5. 母题 教材P14习题A组T2 如图，⊙O是Rt△ABC的内切圆，∠C = 90°。若AC = 12，BC = 9，求⊙O的半径r；若AC = b，BC = a，AB = c，求⊙O的半径r.
　　　　　　　　　　　　　　　　

答案：
[解]如图，设⊙O与AC,AB,BC的切点分别为D,E,F,连接OD,OF;易知OD⊥AC,OF⊥BC.在Rt△ABC中，∠C=90°,AC=12,BC=9,根据勾股定理得AB= $\sqrt{AC^{2}+BC^{2}}$ =15.
　　　　　　　　　　　　　　　　　　
∵在四边形OFCD中,OD=OF,
　　　∠ODC=∠OFC=∠C=90°,
　
∴四边形OFCD是正方形.
　
∴CD=CF=OF=r.
　　　由切线长定理，得AD=AE,BE=BF,
∴CD=CF= $\frac{1}{2}(AC - AE + BC - BE)=\frac{1}{2}(AC + BC - AB)$，即r= $\frac{1}{2}\times(12 + 9 - 15)=3$.
　　　当AC=b,BC=a,AB=c时,r= $\frac{1}{2}(a + b - c)$.

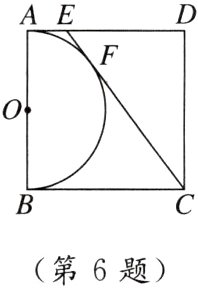
6. 如图，以正方形ABCD的AB边为直径作半圆O，过点C作直线切半圆于点F，交AD边于点E，若△CDE的周长为12，则直角梯形ABCE的周长为（ ）
A. 12
B. 13
C. 14
D. 15
　　　　　　

答案： C　[点拨]设AE的长为x，正方形ABCD的边长为a.
　
∵CE与半圆O相切于点F,易知AD与半圆O相切于点A,BC与半圆O相切于点B.
∴EF=AE=x,BC=CF.
　
∵△CDE的周长=EF+FC+CD+ED=12,
∴AE+ED+CD+BC=12.
∴AD+CD+BC=12.
∴3a=12.
　
∴a=4.
　　　在Rt△CDE中,ED²+CD²=CE²，即(4−x)²+4²=(4+x)²,解得x=1.
　
∴直角梯形ABCE的周长为AE+EF+FC+BC+AB=14.

7. [2024石家庄长安区期末] 如图，在等边三角形DEF的边上分别取点A，B，C，使DA = EB = FC，连接AB，BC，AC. 甲、乙、丙三人的说法如下：
甲：△ABC一定是等边三角形.
乙：若点O是△ABC的外心，则它一定也是△DEF的外心.
丙：若点O是△ABC的中心且AB⊥DE，则AB的长是△DEF的内切圆半径的长的2倍.
则下列判断正确的是（ ）
A. 只有甲的说法正确
B. 只有丙的说法不正确
C. 只有乙的说法不正确
D. 甲、乙、丙的说法都正确
　　　　　

答案：
D　[点拨]
∵△DEF是等边三角形，
　
∴∠DEF=∠EFD=∠FDE=60°,DE=EF=DF.
　
∵DA=EB=FC,
∴AE=BF=CD.
　
∴△ADC≌△BEA≌△CFB(SAS).
∴AC=BA=CB.
　
∴△ABC是等边三角形.
∴甲的说法正确;
　　　如图①,连接OF,OD,OE,OA,OB,OC,
　
∵△ADC≌△BEA,
∴∠DAC=∠EBA.
　
∵点O为△ABC的外心，
　
∴OA=OB.易得∠OAC=∠OBA,
∴∠DAO=∠EBO.又
∵DA=EB,
∴△DAO≌△EBO(SAS).
∴OD=OE.
　　　同理,OF=OE,
∴OF=OE=OD.
　
∴点O也是△DEF的外心.
∴乙的说法正确;
　　　易知点O是△DEF的内心，
　　　　　
　　　如图②,过点O作OH⊥DE于点H,连接OE,则∠OEH=30°,
　
∴在Rt△EOH中,OE=2OH,
∴EH= $\sqrt{3}$OH.
∵OH⊥DE,
∴DE=2EH=2 $\sqrt{3}$OH,即OH= $\frac{\sqrt{3}}{6}$DE.
∵AB⊥DE,∠AEB=60°,
∴AB= $\sqrt{3}$EA,EA= $\frac{1}{2}$EB.
∵DA=EB,
∴EA= $\frac{1}{2}$DA,
∴EA= $\frac{1}{3}$DE.
∴AB= $\sqrt{3}$EA= $\frac{\sqrt{3}}{3}$DE.
∴OH= $\frac{1}{2}$AB,即AB=2OH.
∴AB的长是△DEF的内切圆半径的长的2倍.
∴丙的说法正确