《2025年综合应用创新题典中点九年级数学下册冀教版》

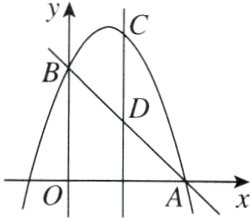
16. 新视角 存在性探究题 [2024·泸州]如图，在平面直角坐标系$xOy$中，已知抛物线$y = ax^{2} + bx + 3$经过点$A(3,0)$，与$y$轴交于点$B$，且关于直线$x = 1$对称.
（1）求该抛物线的表达式.
（2）当$-1\leq x\leq t$时，$y$的取值范围是$0\leq y\leq2t - 1$，求$t$的值.
（3）点$C$是抛物线上位于第一象限的一个动点，过点$C$作$x$轴的垂线交直线$AB$于点$D$，在$y$轴上是否存在点$E$，使得以$B$，$C$，$D$，$E$为顶点的四边形是菱形？若存在，求出该菱形的边长；若不存在，说明理由.

答案：
[解]
(1)
∵A(3，0)，抛物线的对称轴为直线x = 1，
∴抛物线和x轴的另外一个交点为(−1，0)。将(3，0)，(−1，0)代入y = ax² + bx + 3，得$\begin{cases}9a + 3b + 3 = 0\\a - b + 3 = 0\end{cases}$
解得$\begin{cases}a = -1\\b = 2\end{cases}$，则抛物线的表达式为y = -x² + 2x + 3。
(2)
∵当−1≤x≤t时，y的最小值为0，
∴易得−1≤t≤3。
若−1≤t＜1，则当x = t时，y取得最大值，即−t² + 2t + 3 = 2t - 1，解得t₁ = 2(舍去)，t₂ = -2(舍去)。
若1≤t≤3，则当x = 1时y取得最大值，即2t - 1 = -1 + 2 + 3，解得t = 2.5。
综上，t的值为2.5。
(3)存在。
由抛物线的表达式知，点B(0，3)，
由点A，B的坐标求得直线AB的表达式为y = -x + 3，
设点C(x，-x² + 2x + 3)，
则点D(x，-x + 3)，则CD = -x² + 2x + 3 - (-x + 3) = -x² + 3x。
如图，当BD是边时，对应菱形为四边形BDCE'，
则CD = BD。
易知BD = $\sqrt{2}$x，
∴-x² + 3x = $\sqrt{2}$x。
解得x₁ = 3 - $\sqrt{2}$，x₂ = 0(舍去)，
则BD = $\sqrt{2}$x = 3$\sqrt{2}$ - 2，即菱形的边长为3$\sqrt{2}$ - 2。
如图，当BC为边时，同理可得BC = CD，易知BC² = x² + (-x² + 2x)²，则x² + (-x² + 2x)² = (-x² + 3x)²，解得x = 2(不合题意的值已舍去)，
则CD = -2² + 3×2 = 2，即菱形的边长为2。
综上，菱形的边长为3$\sqrt{2}$ - 2或2。

17. 新视角 新定义型题 如图①，已知抛物线$L_{3}:y = 2x^{2} - 8x + 4$与$y$轴交于点$C$，设点$C$关于$L_{3}$的对称轴对称的点为$D$.
（1）求$L_{3}$的顶点坐标和点$D$的坐标.
（2）如图②，若抛物线$L_{1}$的顶点$A$在抛物线$L_{2}$上，抛物线$L_{2}$的顶点$B$在抛物线$L_{1}$上（点$A$，$B$不重合），我们把这样的两条抛物线$L_{1}$，$L_{2}$互称为“伴随抛物线”.
①求以点$D$为顶点的$L_{3}$的“伴随抛物线”$L_{4}$的表达式，并指出$L_{3}$与$L_{4}$中$y$都随$x$的增大而增大的自变量的取值范围；
②将①中的$L_{3}$和$L_{4}$围成的封闭图形（含边界）记为$G$. 若直线$y = kx$将$G$边界上的整点（横、纵坐标都是整数）平分，直接写出$k$的取值范围.

答案：
[解]
(1)
∵抛物线L₃:y = 2x²−8x + 4，
∴y = 2(x - 2)²−4。
∴L₃的顶点坐标为(2，−4)，对称轴为直线x = 2。
若x = 0，则y = 4，
∴C(0，4)。
∴点C关于该抛物线的对称轴对称的点D的坐标为(4，4)。
(2)①
∵L₄的顶点为D(4，4)，
∴设抛物线L₄的表达式为y = a(x - 4)² + 4(a≠0)。
∵L₄过点(2，−4)，
∴a(2 - 4)² + 4 = -4，
∴a = -2。
∴L₄的表达式为y = -2(x - 4)² + 4，即y = -2x² + 16x - 28。
画出L₄如图，由图可知当2≤x≤4时，L₃与L₄中y都随x的增大而增大。
②−$\frac{2}{3}$＜k＜$\frac{2}{3}$。[点拨]L₃和L₄组成的图形G如图所示，则易得G边界上的整点有4个，分别为(2，−4)，(3，−2)，(3，2)，(4，4)。
∵y = kx是过原点的直线，且将图形G上的整点平分，
∴直线y = kx在(3，−2)，(3，2)之间。分别把两点的坐标代入得−2 = 3k，则k = -$\frac{2}{3}$，2 = 3k，则k = $\frac{2}{3}$。
∴k的取值范围为-$\frac{2}{3}$＜k＜$\frac{2}{3}$。