《2025年综合应用创新题典中点九年级数学下册冀教版》

1. 母题教材P7习题A组T1在同一平面内，已知⊙O的半径为4，圆心O到直线l的距离为6，P为圆上的一个动点，则点P到直线l的距离不可能是 ( )
A. 2
B. 6
C. 10
D. 14

答案： D

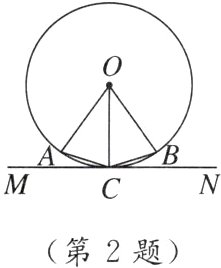
2. [2024福建]如图，已知点A，B在⊙O上，∠AOB=72°，直线MN与⊙O相切，切点为C，且C为⌢AB的中点，则∠ACM等于 ( )
A. 18° B. 30° C. 36° D. 72°
　　　　

答案： A

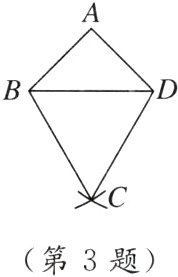
3. 如图，在△ABD中，∠A=90°，AB=AD，分别以点B和点D为圆心，BD长为半径画弧，交于点C，连接BC，DC，若AB=5$\sqrt{6}$，则△ABD的外心与△BCD的内心的距离是 ( )
A. $\frac{10}{3}$$\sqrt{3}$ B. 5$\sqrt{3}$ C. $\frac{10}{3}$ D. 5
　　　　

答案： D

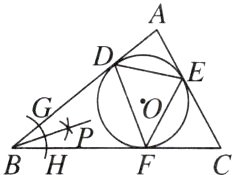
4. 多选题如图，△ABC的内切圆(圆心为点O)与各边分别相切于点D，E，F，连接EF，DE，DF.以点B为圆心，适当长为半径作弧分别交AB，BC于G，H两点；分别以点G，H为圆心，大于$\frac{1}{2}$GH的长为半径作弧，两条弧交于点P；作射线BP.下列说法正确的是 ( )
A. 射线BP一定过点O
B. 点O是△DEF三条中线的交点
C. 若△ABC是等边三角形，则DE=$\frac{1}{2}$BC
D. 点O不是△DEF三条边的垂直平分线的交点
　　　　　　　　　　　　　　　

答案： AC 【点拨】
∵⊙O是△ABC的内切圆，
∴点O是△ABC三条角平分线的交点. 由尺规作图可知，射线BP是∠ABC的平分线.
∴射线BP一定过点O，故A选项说法正确，符合题意；点O是△DEF三条边的垂直平分线的交点，故B，D选项说法错误，不符合题意；
∵△ABC是等边三角形，
∴点D，E分别为AB，AC的中点.
∴DE是△ABC的中位线.
∴DE = $\frac{1}{2}$BC，故C选项说法正确，符合题意.

5. 情境题生活应用如图是高铁路线在转向处所设计的圆曲线(即圆弧)，列车在转弯时经过的曲线起点为A，终点为B，过点A，B的两条切线相交于点C，列车在从A到B行驶的过程中转角α为60°，则∠AOB的度数为 ( )
　　　　　　　　　
A. 40°
B. 50°
C. 60°
D. 70°

答案： C 【点拨】
∵∠α = 60°，
∴∠ACB = 180° - 60° = 120°.
∵AC，BC是切线，
∴∠CAO = ∠CBO = 90°.
∴∠AOB = 360° - ∠ACB - ∠CAO - ∠CBO = 360° - 120° - 90° - 90° = 60°.

6. [2024唐山期末]白老师布置了如下题目:“如图，以AB为直径的半圆O上有一点C，且∠CBA=30°，AB=8，M为直径AB上一动点，点N与点M关于直线AC对称，MP⊥MN于点M，交NC的延长线于点P.”要求同学们添加一个条件，提出问题，并给出相应问题的答案，则下列两名同学中说法正确的是 ( )
嘉嘉:当AM=2时，NP与半圆O相切.
琪琪:若点P恰好落在弧BC上时，则AM=4.
A. 嘉嘉 B. 琪琪
C. 嘉嘉和琪琪 D. 两人都不正确
　　　　　　 　

答案：
C 【点拨】如图①，当AM = 2时，连接OC，CM.
∵∠CBA = 30°，
∴∠AOC = 60°. 又
∵OA = OC，
∴△OAC是等边三角形.

∴∠ACO = 60°.
∵AB = 8，
∴OA = 4.
∵AM = 2，
∴OM = 2.
∴AM = OM.
∴∠ACM = ∠OCM = 30°.
∵点N与点M关于直线AC对称，
∴∠NCA = ∠MCA = 30°，
∴∠NCO = 90°.
∴OC⊥PN.
∵OC是半圆O的半径，
∴NP与半圆O相切.
∴嘉嘉正确；
如图②，当点P恰好落在弧BC上时，连接AP，BP，CM，设AC与MN交于点G，PM与BC交于点H.
∵点N与点M关于直线AC对称，
∴CM = CN.
∴∠N = ∠CMN.
∵PM⊥MN，
∴∠PMN = 90°.
∴∠N + ∠NPM = ∠CMN + ∠CMP = 90°.
∴∠CPM = ∠CMP.
∴CM = CP.
∴CM = CN = CP.
∵点N与点M关于直线AC对称，
∴AC⊥MN.
∴∠AGM = 90°，
∵AB是半圆O的直径，
∴∠ACB = 90°.
∴∠AGM = ∠ACB.
∴MN//BC.
∴$\frac{PH}{HM}=\frac{PC}{CN}=1$.
∴PH = MH. 易知BC是PM的垂直平分线.
∴BP = BM.
∴∠PBM = 2∠CBA = 60°.
∵AB是半圆O的直径，
∴∠APB = 90°.
∴PB = AB·cos 60° = 8×$\frac{1}{2}$ = 4.
∴BM = BP = 4.
∴AM = AB - BM = 4.
∴琪琪正确.

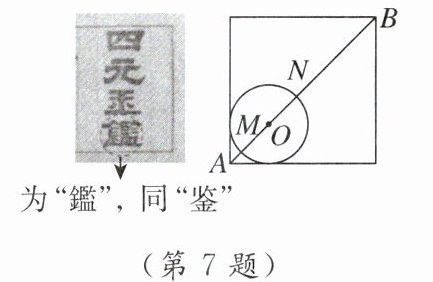
7. 新考向数学文化中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段，一角圆池占之”意思是说:一块正方形田地，在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)，如图所示.问题:此图中，正方形一条对角线AB与⊙O相交于点M，N(点N在点M的右上方).若AB的长度为10丈，⊙O的半径为2丈，则BN的长度为_______丈.

答案： (8 - 2$\sqrt{2}$)