第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
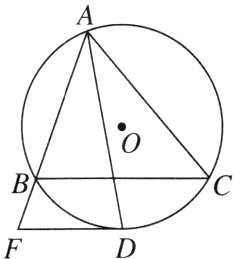
5. [2024德阳] 如图,已知⊙O的半径为5,B,C是⊙O上两定点,点A是⊙O上一动点,且∠BAC = 60°,∠BAC的平分线交⊙O于点D.
(1)证明:点D为BC上一定点;
(2)过点D作BC的平行线交AB的延长线于点F.
①判断DF与⊙O的位置关系,并说明理由;
②若△ABC为锐角三角形,求DF的取值范围.
(1)证明:点D为BC上一定点;
(2)过点D作BC的平行线交AB的延长线于点F.
①判断DF与⊙O的位置关系,并说明理由;
②若△ABC为锐角三角形,求DF的取值范围.

答案:
(1)【证明】连接OB,OD,如图①,
∵∠BAC = 60°,∠BAC的平分线交⊙O于点D,
∴∠BAD = $\frac{1}{2}$∠BAC = 30°.
∴∠BOD = 2∠BAD = 60°.
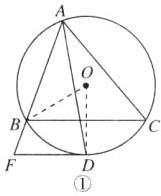
∴BD所对的圆心角的度数是60°.
∵B为定点,
∴点D为BC上一定点.
(2)【解】①DF与⊙O相切.理由如下:
∵∠BAC的平分线交⊙O于点D,
∴∠BAD = ∠CAD.
∴BD = CD.
∴OD⊥BC.
∵DF//BC,
∴OD⊥DF.
∵OD为⊙O的半径,
∴DF与⊙O相切.
②当∠A₁BC为直角时,连接OD交BC于点M,如图②,
∵∠A₁BC = 90°,∠BA₁C = 60°,
∴∠C = 30°,A₁C为⊙O的直径.
∵⊙O的半径为5,
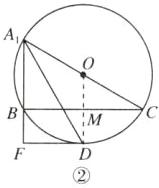
∴A₁C = 10.
∴A₁B = $\frac{1}{2}$A₁C = 5.
∴BC = $\sqrt{A₁C² - A₁B²}$ = 5$\sqrt{3}$.
由①知,BD = CD,OD⊥BC,
∴BM = $\frac{1}{2}$BC = $\frac{5\sqrt{3}}{2}$,∠BMD = 90°.
∵DF与⊙O相切,
∴∠FDM = 90°.
∵∠FBC = 180° - ∠A₁BC = 90°,
∴四边形BFDM是矩形.
∴DF = BM = $\frac{5\sqrt{3}}{2}$.
当∠A₂CB为直角时,连接OD,如图③,
∵∠A₂CB = 90°,∠BA₂C = 60°,
∴A₂B是⊙O的直径,∠A₂BC = 30°.
∵DF//BC,
∴∠F = ∠A₂BC = 30°.
∵DF与⊙O相切,
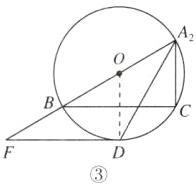
∴∠FDO = 90°.
∴在Rt△ODF中,OF = 2OD = 10.
∴DF = $\sqrt{OF² - OD²}$ = $\sqrt{10² - 5²}$ = 5$\sqrt{3}$.
易知,当A由A₁运动到A₂(不包括A₁,A₂)时,△ABC是锐角三角形,
∴DF的取值范围是$\frac{5\sqrt{3}}{2}$ < DF < 5$\sqrt{3}$.
(1)【证明】连接OB,OD,如图①,
∵∠BAC = 60°,∠BAC的平分线交⊙O于点D,
∴∠BAD = $\frac{1}{2}$∠BAC = 30°.
∴∠BOD = 2∠BAD = 60°.

∴BD所对的圆心角的度数是60°.
∵B为定点,
∴点D为BC上一定点.
(2)【解】①DF与⊙O相切.理由如下:
∵∠BAC的平分线交⊙O于点D,
∴∠BAD = ∠CAD.
∴BD = CD.
∴OD⊥BC.
∵DF//BC,
∴OD⊥DF.
∵OD为⊙O的半径,
∴DF与⊙O相切.
②当∠A₁BC为直角时,连接OD交BC于点M,如图②,
∵∠A₁BC = 90°,∠BA₁C = 60°,
∴∠C = 30°,A₁C为⊙O的直径.
∵⊙O的半径为5,

∴A₁C = 10.
∴A₁B = $\frac{1}{2}$A₁C = 5.
∴BC = $\sqrt{A₁C² - A₁B²}$ = 5$\sqrt{3}$.
由①知,BD = CD,OD⊥BC,
∴BM = $\frac{1}{2}$BC = $\frac{5\sqrt{3}}{2}$,∠BMD = 90°.
∵DF与⊙O相切,
∴∠FDM = 90°.
∵∠FBC = 180° - ∠A₁BC = 90°,
∴四边形BFDM是矩形.
∴DF = BM = $\frac{5\sqrt{3}}{2}$.
当∠A₂CB为直角时,连接OD,如图③,
∵∠A₂CB = 90°,∠BA₂C = 60°,
∴A₂B是⊙O的直径,∠A₂BC = 30°.
∵DF//BC,
∴∠F = ∠A₂BC = 30°.
∵DF与⊙O相切,

∴∠FDO = 90°.
∴在Rt△ODF中,OF = 2OD = 10.
∴DF = $\sqrt{OF² - OD²}$ = $\sqrt{10² - 5²}$ = 5$\sqrt{3}$.
易知,当A由A₁运动到A₂(不包括A₁,A₂)时,△ABC是锐角三角形,
∴DF的取值范围是$\frac{5\sqrt{3}}{2}$ < DF < 5$\sqrt{3}$.
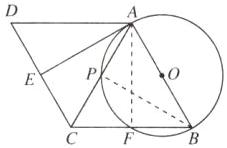
6. 如图,四边形ABCD是菱形,以AB为直径作⊙O,交CB于点F,点E在CD上,且CE = CF,连接AE,AC,AC交⊙O于点P.
(1)求证:AE是⊙O的切线;
(2)若AP = √3,BF = 1,求⊙O的半径.

(1)求证:AE是⊙O的切线;
(2)若AP = √3,BF = 1,求⊙O的半径.

答案:
(1)【证明】如图,连接AF.
∵四边形ABCD为菱形,
∴∠ACF = ∠ACE.
又
∵CF = CE,AC = AC,
∴△ACF≌△ACE(SAS).
∴∠AFC = ∠AEC.
∵AB是⊙O的直径,
∴∠AFB = 90°.
∴∠AFC = 90°.
∴∠AEC = 90°.
易知AB//DC,
∴∠BAE + ∠AEC = 180°.
∴∠BAE = 90°.
∴OA⊥AE.
∵OA是⊙O的半径,
∴AE是⊙O的切线.
(2)【解】如图,连接BP.
∵AB是⊙O的直径,
∴∠APB = 90°,即BP⊥AC.
易知AB = CB,又
∵AP = $\sqrt{3}$,
∴AC = 2AP = 2$\sqrt{3}$.
设⊙O的半径为R,则AB = 2R,
∴BC = 2R,
∴CF = 2R - 1.
∵AC² - CF² = AF²,AB² - BF² = AF²,
∴AC² - CF² = AB² - BF².
∴(2$\sqrt{3}$)² - (2R - 1)² = (2R)² - 1².
解得R = $\frac{3}{2}$(负值已舍去).
∴⊙O的半径为$\frac{3}{2}$.
(1)【证明】如图,连接AF.
∵四边形ABCD为菱形,
∴∠ACF = ∠ACE.

又
∵CF = CE,AC = AC,
∴△ACF≌△ACE(SAS).
∴∠AFC = ∠AEC.
∵AB是⊙O的直径,
∴∠AFB = 90°.
∴∠AFC = 90°.
∴∠AEC = 90°.
易知AB//DC,
∴∠BAE + ∠AEC = 180°.
∴∠BAE = 90°.
∴OA⊥AE.
∵OA是⊙O的半径,
∴AE是⊙O的切线.
(2)【解】如图,连接BP.
∵AB是⊙O的直径,
∴∠APB = 90°,即BP⊥AC.
易知AB = CB,又
∵AP = $\sqrt{3}$,
∴AC = 2AP = 2$\sqrt{3}$.
设⊙O的半径为R,则AB = 2R,
∴BC = 2R,
∴CF = 2R - 1.
∵AC² - CF² = AF²,AB² - BF² = AF²,
∴AC² - CF² = AB² - BF².
∴(2$\sqrt{3}$)² - (2R - 1)² = (2R)² - 1².
解得R = $\frac{3}{2}$(负值已舍去).
∴⊙O的半径为$\frac{3}{2}$.
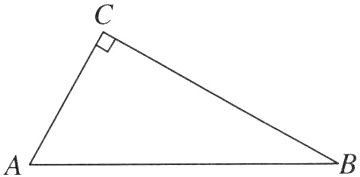
7. [2024广东] 如图,在△ABC中,∠C = 90°.
(1)实践与操作:用尺规作图法作∠A的平分线AD交BC于点D(保留作图痕迹,不要求写作法);
(2)应用与证明:在(1)的条件下,以点D为圆心,DC长为半径作⊙D. 求证:AB与⊙D相切.
(1)实践与操作:用尺规作图法作∠A的平分线AD交BC于点D(保留作图痕迹,不要求写作法);
(2)应用与证明:在(1)的条件下,以点D为圆心,DC长为半径作⊙D. 求证:AB与⊙D相切.

答案:
(1)【解】如图,AD即为所求.
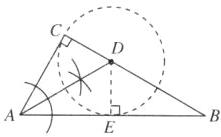
(2)【证明】如图,作⊙D,过点D作DE⊥AB于点E.
∵∠C = 90°,
∴DC⊥AC.
∵AD平分∠BAC,
∴DE = CD.
∴DE为⊙D的半径.
∴AB与⊙D相切.
(1)【解】如图,AD即为所求.

(2)【证明】如图,作⊙D,过点D作DE⊥AB于点E.
∵∠C = 90°,
∴DC⊥AC.
∵AD平分∠BAC,
∴DE = CD.
∴DE为⊙D的半径.
∴AB与⊙D相切.
查看更多完整答案,请扫码查看


