《2025年综合应用创新题典中点九年级数学下册冀教版》

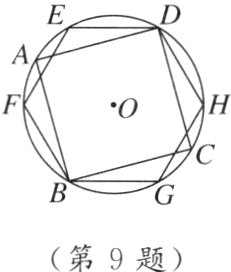
9. [2024保定期末] 如图，半径为1的⊙O是正方形ABCD，正六边形DEFbGH的外接圆，则$\overset{\frown}{AE}$的长为 （ ）
A. $\frac{\pi}{3}$ B. $\frac{\pi}{6}$ C. $\frac{\pi}{12}$ D. $\frac{\pi}{24}$
　　　

答案：
B　[点拨]如图,连接OE,OF,则∠EOF = $\frac{360°}{6}$ = 60°.
∵半径为1的⊙O是正方形ABCD，正六边形DEFGBH的外接圆，
∴$\overset{\frown}{AD}$ = $\overset{\frown}{AB}$，$\overset{\frown}{DE}$ = $\overset{\frown}{BF}$，
∴$\overset{\frown}{AF}$ = $\overset{\frown}{AE}$ = $\frac{1}{2}$$\overset{\frown}{EF}$.
　　　　　　　　　　　　　　　　　
∵$\overset{\frown}{EF}$的长为$\frac{60π×1}{180}$ = $\frac{π}{3}$，
∴$\overset{\frown}{AE}$的长为$\frac{π}{6}$.

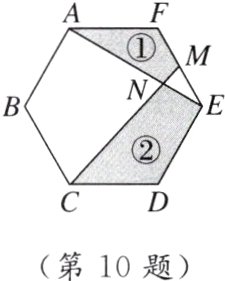
10. [2024邯郸模拟] 如图所示的正六边形ABCDEF中，点M是边EF的中点，连接AE，CM，相交于点N. 若正六边形ABCDEF的面积为6，阴影部分①的面积为a，阴影部分②的面积为b，则b - a的值是 （ ）
A. $\frac{\sqrt{3}}{2}$ B. 1 C. $\sqrt{3}$ D. 2
　　　

答案：
B　[点拨]连接AD,BE,CF,CE,如图所示，
　　由正六边形的性质可知，S△ABO = S△BCO = S△CDO = S△DEO = S△EFO = S△AFO = 1，∠AOF = ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = 360°÷6 = 60°，
　
∴△AOF,△AOB,△BOC,△COD,△DOE,△EOF是全等的等边三角形.
　
∴四边形AOEF,四边形OCDE是菱形,
　
∴S△AEF = $\frac{1}{2}$S菱形AOEF = $\frac{1}{2}$(S△AFO + S△EFO) = 1.
　　同理，S△CDE = $\frac{1}{2}$S菱形OCDE = $\frac{1}{2}$(S△CDO + S△DEO) = 1.
　
∵S四边形CDEF = S△CDO + S△DEO + S△EFO = S△CDE + S△CEF = 3，
∴S△CEF = 2.
　
∵点M是边EF的中点，
∴S△CFM = S△CEM = 1.
　
∵S四边形CDEM = S△CFM + S四边形CDEM，
∴S四边形CDEM = 3 - 1 = 2.
　
∴b - a = (b + S△NME) - (a + S△NME) = S四边形CDEM - S△AEF = 2 - 1 = 1.
　　　　　　　　　　　　　　　　　

11. 如图，⊙O与正六边形ABCDEF的边CD，EF分别相切于点C，F. 若AB = 2，则⊙O的半径长为________.
　　　　　　　

答案：
$\frac{4\sqrt{3}}{3}$　[点拨]如图,连接CF,OC,OF,过点D作DG⊥
CF于点G,过点E作EH⊥CF于点H,则EH//DG.
　
∵EF,CD是⊙O的切线,
　
∴∠OFE=∠OCD=90°.
　　　　　　　　　　　　　　　　　
　
∵多边形ABCDEF是正六边形，
　
∴∠FED=∠CDE=120°.
　
∴易得∠COF=120°.
　
∵OC=OF,
∴∠OCF=∠OFC=30°.
　
∴∠EFH=∠DCG=60°.
　
∵∠EHF=∠DGC=90°,CD=EF,
　
∴△CDG≌△FEH(AAS).
∴FH=CG,EH=DG.
　
∴四边形EHGD是矩形.
∴HG=DE=2.
　
∵EF=CD=2、∠DCG=∠EFH=60°,
　
∴易得FH=CG = $\frac{1}{2}$EF = 1.
∴CF=4.
　　过点O作OM⊥CF于点M,
　　则CM = $\frac{1}{2}$CF = 2，
∴OC = $\frac{CM}{\cos30°}$ = $\frac{2}{\frac{\sqrt{3}}{2}}$ = $\frac{4\sqrt{3}}{3}$.
　
∴⊙O的半径长为$\frac{4\sqrt{3}}{3}$.

12. 如图，正六边形ABCDEF内接于⊙O.
（1）若P是$\overset{\frown}{CD}$上一动点，连接BP，FP，求∠BPF的度数.
（2）已知△ADF的面积为2$\sqrt{3}$.
①求∠DAF的度数；
②求⊙O的半径.
　　　　　　　　　　　　　

答案：
[解]
(1)如图所示，连接AP,FO.
　
∵六边形ABCDEF是正六边形，
　
∴AF=AB,∠AOF = $\frac{360°}{6}$ = 60°.
　　　　　　　　　　　　　　　　　
　
∴∠APF = $\frac{1}{2}$∠AOF = 30°.
　
∵AF = AB，
∴$\overset{\frown}{AF}$ = $\overset{\frown}{AB}$，
∴∠APB = ∠APF = 30°.
　
∴∠BPF = ∠APB + ∠APF = 60°.
(2)①
∵∠AOF = 60°，AO = FO，
　
∴△AOF是等边三角形.
∴∠DAF = 60°.
　　②
∵AD为⊙O的直径，
∴∠AFD = 90°.
　
∵∠DAF = 60°，
∴DF = $\sqrt{3}$AF.
　
∴S△ADF = $\frac{1}{2}$AF·DF = $\frac{\sqrt{3}}{2}$AF² = 2$\sqrt{3}$
　
∴AF = 2(负值已舍去).
　
∵△AOF是等边三角形，
∴OF = AF = 2.
　
∴⊙O的半径为2.

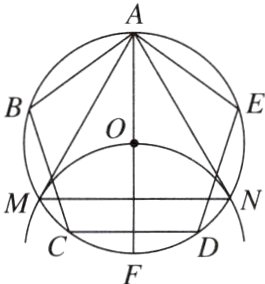
13. 新视角 动手操作题 如图，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答问题：
①作直径AF.
②以点F为圆心，FO的长为半径作圆弧，与⊙O交于点M，N.
③连接AM，MN，NA.
（1）求∠ABC的度数.
（2）△AMN是正三角形吗？请说明理由.
（3）从点A开始，以DN长为半径，在⊙O上依次截取点，再顺次连接这些点，得到正n边形，请直接写出n的值.
　　　　　　　　　　　　　

答案：
[解]
(1)
∵五边形ABCDE是正五边形,
　
∴∠ABC = $\frac{(5 - 2)×180°}{5}$ = 108°.
(2)△AMN是正三角形,
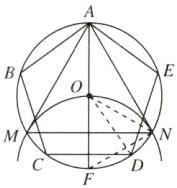
　　理由:如图,连接ON,NF,由题意可得FN=ON=OF,
∴△FON是正三角形.
　
∴∠NFA = 60°.
　
∴∠NMA = 60°.
　　　　　　　　　　　　　　　　　
　　同理可得∠ANM = 60°，
　
∴△MAN是正三角形.
(3)n的值为15.　[点拨]连接OD,如图.
　
∵∠AMN = 60°，
∴∠AON = 120°.
　
∵∠AOD = $\frac{360°}{5}$×2 = 144°，
　
∴∠NOD = ∠AOD - ∠AON = 144° - 120° = 24°.
　
∵360°÷24° = 15，
∴n的值为15.