第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 如图,过⊙O上一点A作⊙O的切线,可以作( )
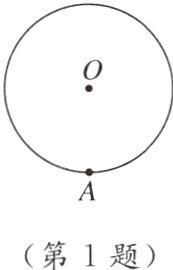
A. 0条
B. 1条
C. 2条
D. 无数条

A. 0条
B. 1条
C. 2条
D. 无数条
答案:
B
2. [2024山西] 如图,已知△ABC,以AB为直径的⊙O交BC于点D,与AC相切于点A,连接OD. 若∠AOD=80°,则∠C的度数为( )
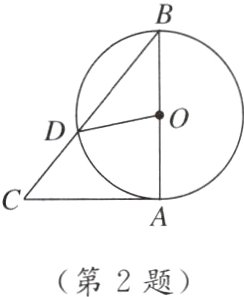
A. 30°
B. 40°
C. 45°
D. 50°

A. 30°
B. 40°
C. 45°
D. 50°
答案:
D
3. 母题 教材P9练习T2 如图,线段AB是⊙O的直径,CD是⊙O的弦,过点C作⊙O的切线交AB的延长线于点E,连接BD,∠E=40°,则∠CDB=( )
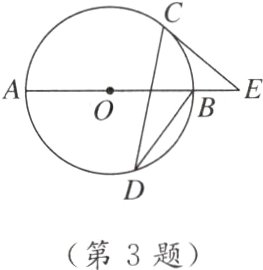
A. 20°
B. 25°
C. 40°
D. 50°

A. 20°
B. 25°
C. 40°
D. 50°
答案:
B
4. 情境题 生活应用 [2024·沧州期末] 如图是一个钟表表盘,连接表示整点2和10的B,D两点并延长,交过表示整点8的点C的切线于点P,若表盘的半径长为$\sqrt{3}$,则PC的长为( )
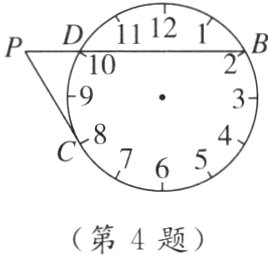
A. 3
B. 2
C. 2$\sqrt{3}$
D. 3$\sqrt{3}$

A. 3
B. 2
C. 2$\sqrt{3}$
D. 3$\sqrt{3}$
答案:
B [点拨]设钟表表盘的中心为点O,连接BC,OD,如图,易知点O在BC上,∠DOC=2×30°=60°,

∴∠DBC=$\frac{1}{2}$∠DOC=30°.
∵PC与⊙O相切于点C,
∴∠BCP=90°.
∵表盘的半径长为$\sqrt{3}$,
∴BC=2$\sqrt{3}$,
∴CP=BC·tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2.
B [点拨]设钟表表盘的中心为点O,连接BC,OD,如图,易知点O在BC上,∠DOC=2×30°=60°,

∴∠DBC=$\frac{1}{2}$∠DOC=30°.
∵PC与⊙O相切于点C,
∴∠BCP=90°.
∵表盘的半径长为$\sqrt{3}$,
∴BC=2$\sqrt{3}$,
∴CP=BC·tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2.
5. [2024石家庄裕华区期末] 如图,点P是⊙O的半径OC的延长线上一点,过点P作⊙O的切线,切点为A,AB是⊙O的弦,连接AC,BC,若∠PAB=70°,则∠ACB的大小为_______.
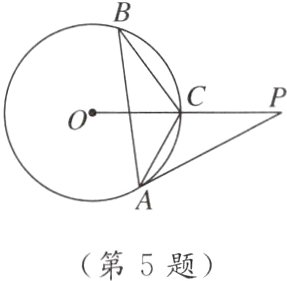

答案:
110°
6. [2024盐城] 如图,点C在以AB为直径的⊙O上,过点C作⊙O的切线l,过点A作AD⊥l,垂足为D,连接AC,BC.
(1)求证:△ABC∽△ACD;
(2)若AC=5,CD=4,求⊙O的半径.
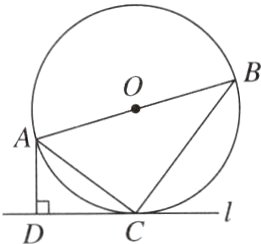
(1)求证:△ABC∽△ACD;
(2)若AC=5,CD=4,求⊙O的半径.

答案:
(1)[证明]连接OC,如图.
∵l是⊙O的切线,
∴OC⊥l.

∵AD⊥l,
∴OC//AD,∠ADC=90°.
∴∠CAD=∠ACO.
∵OA=OC,
∴∠CAB=∠ACO,
∴∠CAD=∠CAB.
∵AB是直径,
∴∠ACB=90°.
∴∠ADC=∠ACB=90°.
∴△ABC∽△ACD.
(2)[解]
∵AC=5,CD=4,∠ADC=90°,
∴AD=$\sqrt{AC^{2}-CD^{2}}$=3.
∵△ABC∽△ACD,
∴$\frac{AB}{AC}$=$\frac{AC}{AD}$.
即$\frac{AB}{5}$=$\frac{5}{3}$.
∴AB=$\frac{25}{3}$.
∴⊙O的半径为$\frac{25}{6}$.
(1)[证明]连接OC,如图.
∵l是⊙O的切线,
∴OC⊥l.

∵AD⊥l,
∴OC//AD,∠ADC=90°.
∴∠CAD=∠ACO.
∵OA=OC,
∴∠CAB=∠ACO,
∴∠CAD=∠CAB.
∵AB是直径,
∴∠ACB=90°.
∴∠ADC=∠ACB=90°.
∴△ABC∽△ACD.
(2)[解]
∵AC=5,CD=4,∠ADC=90°,
∴AD=$\sqrt{AC^{2}-CD^{2}}$=3.
∵△ABC∽△ACD,
∴$\frac{AB}{AC}$=$\frac{AC}{AD}$.
即$\frac{AB}{5}$=$\frac{5}{3}$.
∴AB=$\frac{25}{3}$.
∴⊙O的半径为$\frac{25}{6}$.
7. 如图,将量角器和一块含30°角的直角三角尺紧靠着放在同一平面内,使D,C,B在同一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,则点E在量角器上所对应的锐角度数是( )
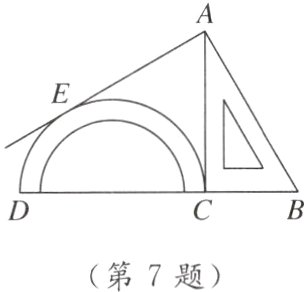
A. 60°
B. 45°
C. 75°
D. 50°

A. 60°
B. 45°
C. 75°
D. 50°
答案:
A [点拨]如图,设量角器的圆心为O,连接OA,OE.
∵CD=2OC=2BC,
∴OC=BC;
∵∠ACB=90°,
∴AC⊥OB,

∴OA=BA.
∴∠AOC=∠ABC=60°.
∵AE是切线,OE是半径,
∴∠AEO=90°.
∴∠AEO=∠ACO=90°.
∵OA=OA,OE=OC,
∴Rt△AOE≌Rt△AOC.
∴∠AOE=∠AOC=60°.
∴∠EOD=180°−60°−60°=60°,故选A.
A [点拨]如图,设量角器的圆心为O,连接OA,OE.
∵CD=2OC=2BC,
∴OC=BC;
∵∠ACB=90°,
∴AC⊥OB,

∴OA=BA.
∴∠AOC=∠ABC=60°.
∵AE是切线,OE是半径,
∴∠AEO=90°.
∴∠AEO=∠ACO=90°.
∵OA=OA,OE=OC,
∴Rt△AOE≌Rt△AOC.
∴∠AOE=∠AOC=60°.
∴∠EOD=180°−60°−60°=60°,故选A.
8. 母题 教材P21复习题A组T6 如图,在平面直角坐标系中,⊙M与x轴相切于点A,与y轴交于点B,C. 若圆心M的坐标是(4,5),则弦BC的长度为( )
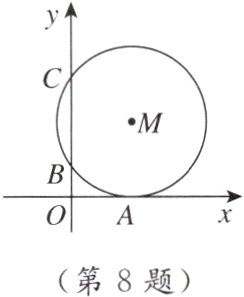
A. 3
B. 4
C. 5
D. 6

A. 3
B. 4
C. 5
D. 6
答案:
D [点拨]如图,连接MA,MB,过点M作MN⊥y轴,
垂足为N,则BN=CN=$\frac{1}{2}$BC.
∵⊙M与x轴相切于点A,
∴MA⊥x轴.
∵圆心M的坐标是(4,5),
∴MA=5,MN=4.
∴MB=MA=5.
∴在Rt△BMN中,BN=$\sqrt{MB^{2}-MN^{2}}$=$\sqrt{5^{2}-4^{2}}$=3.
∴BC=2BN=6.

D [点拨]如图,连接MA,MB,过点M作MN⊥y轴,
垂足为N,则BN=CN=$\frac{1}{2}$BC.
∵⊙M与x轴相切于点A,
∴MA⊥x轴.
∵圆心M的坐标是(4,5),
∴MA=5,MN=4.
∴MB=MA=5.
∴在Rt△BMN中,BN=$\sqrt{MB^{2}-MN^{2}}$=$\sqrt{5^{2}-4^{2}}$=3.
∴BC=2BN=6.

查看更多完整答案,请扫码查看


