第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 如图,在△ABC中,AB = 3,AC = 4,BC = 5,作∠ABC的平分线交AC于点D,以点D为圆心,DA长为半径作圆,与射线BD交于点E,F. 有下列结论:①△ABC是直角三角形;②⊙D与直线BC相切;③tan∠CDF = 2. 其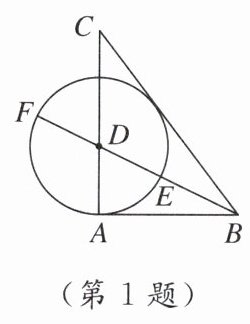
中正确的结论有( )
A. ①
B. ①②
C. ①②③
D. ①③

中正确的结论有( )
A. ①
B. ①②
C. ①②③
D. ①③
答案:
C [点拨]如图,作DG⊥BC于点G.
∵AB=3,AC=4,BC=5,
∴AB²+AC²=25=BC².
∴△ABC是直角三角形,且∠CAB=90°,故①正确.
∵DG⊥BC,DA⊥BA,且BD平分∠ABC,
∴DG=DA.
∴DG是⊙D的半径
∴⊙D与直线BC相切,故②正确
设DG=DA=r.
∵$\frac{1}{2}$BC·DG+$\frac{1}{2}$AB·DA=$\frac{1}{2}$AB·AC=S△ABC,
∴$\frac{1}{2}$×5r+$\frac{1}{2}$×3r=$\frac{1}{2}$×3×4.解得r=$\frac{3}{2}$.
∴DA=$\frac{3}{2}$.
∵∠CDF=∠BDA,
∴tan∠CDF=tan∠BDA=$\frac{AB}{DA}$=$\frac{3}{\frac{3}{2}}$=2,故③正确.

C [点拨]如图,作DG⊥BC于点G.
∵AB=3,AC=4,BC=5,
∴AB²+AC²=25=BC².
∴△ABC是直角三角形,且∠CAB=90°,故①正确.
∵DG⊥BC,DA⊥BA,且BD平分∠ABC,
∴DG=DA.
∴DG是⊙D的半径
∴⊙D与直线BC相切,故②正确
设DG=DA=r.
∵$\frac{1}{2}$BC·DG+$\frac{1}{2}$AB·DA=$\frac{1}{2}$AB·AC=S△ABC,
∴$\frac{1}{2}$×5r+$\frac{1}{2}$×3r=$\frac{1}{2}$×3×4.解得r=$\frac{3}{2}$.
∴DA=$\frac{3}{2}$.
∵∠CDF=∠BDA,
∴tan∠CDF=tan∠BDA=$\frac{AB}{DA}$=$\frac{3}{\frac{3}{2}}$=2,故③正确.

2. 如图①,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ = QB = 1,动点A在PQ上方的⊙O上运动(含P,Q两点),连接OA,AB,设∠AOB = α. 有以下结论:结论Ⅰ:当线段AB与⊙O只有一个公共点A时,α的范围是0°≤α≤60°;结论Ⅱ:当线段AB与⊙O有两个公共点A,M时,如图②,若AO⊥PM于点D,则tan∠MPQ = $\frac{\sqrt{15}}{15}$. 下列判断正确的是( )

A. Ⅰ和Ⅱ都正确
B. Ⅰ和Ⅱ都错误
C. Ⅰ错误,Ⅱ正确
D. Ⅰ正确,Ⅱ错误

A. Ⅰ和Ⅱ都正确
B. Ⅰ和Ⅱ都错误
C. Ⅰ错误,Ⅱ正确
D. Ⅰ正确,Ⅱ错误
答案:
A [点拨]结论I:当点A与点Q重合时,
线段AB与⊙O只有一个公共点A,此时α=0°;
当线段AB所在的直线与⊙O相切时,如图①所示,
线段AB与⊙O只有一个公共点A,
此时OA⊥BA,OA=1,OB=OQ+QB=2,
∴cos∠AOB=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴∠AOB=α=60°.
∴当线段AB与⊙O只有一个公共点A时,α的范围是0°≤α≤60°,故结论I正确.
结论II:连接MQ,如图②所示,
∵PQ是⊙O的直径,
∴∠PMQ=90°.
∵OA⊥PM,
∴∠PDO=90°.
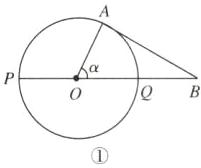
∴∠PDO=∠PMQ.
∴OD//MQ.
∴△PDO∽△PMQ.
∴$\frac{PD}{PM}$=$\frac{DO}{MQ}$=$\frac{PO}{PQ}$.
∵PO=OQ=$\frac{1}{2}$PQ,
∴DO=$\frac{1}{2}$MQ,PD=$\frac{1}{2}$PM.
同理可得MQ=$\frac{1}{2}$AO,BM=$\frac{1}{2}$AB.
∵AO=1,
∴MQ=$\frac{1}{2}$.
∴OD=$\frac{1}{4}$.
∴在Rt△PDO中,PD=$\sqrt{PO^{2}-OD^{2}}$=$\frac{\sqrt{15}}{4}$.
∴PM=$\frac{\sqrt{15}}{2}$.
∴tan∠MPQ=$\frac{MQ}{PM}$=$\frac{\frac{1}{2}}{\frac{\sqrt{15}}{2}}$=$\frac{\sqrt{15}}{15}$.故结论II正确.
A [点拨]结论I:当点A与点Q重合时,
线段AB与⊙O只有一个公共点A,此时α=0°;
当线段AB所在的直线与⊙O相切时,如图①所示,
线段AB与⊙O只有一个公共点A,
此时OA⊥BA,OA=1,OB=OQ+QB=2,
∴cos∠AOB=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴∠AOB=α=60°.
∴当线段AB与⊙O只有一个公共点A时,α的范围是0°≤α≤60°,故结论I正确.
结论II:连接MQ,如图②所示,
∵PQ是⊙O的直径,
∴∠PMQ=90°.
∵OA⊥PM,
∴∠PDO=90°.

∴∠PDO=∠PMQ.
∴OD//MQ.
∴△PDO∽△PMQ.
∴$\frac{PD}{PM}$=$\frac{DO}{MQ}$=$\frac{PO}{PQ}$.
∵PO=OQ=$\frac{1}{2}$PQ,
∴DO=$\frac{1}{2}$MQ,PD=$\frac{1}{2}$PM.
同理可得MQ=$\frac{1}{2}$AO,BM=$\frac{1}{2}$AB.
∵AO=1,
∴MQ=$\frac{1}{2}$.
∴OD=$\frac{1}{4}$.
∴在Rt△PDO中,PD=$\sqrt{PO^{2}-OD^{2}}$=$\frac{\sqrt{15}}{4}$.
∴PM=$\frac{\sqrt{15}}{2}$.
∴tan∠MPQ=$\frac{MQ}{PM}$=$\frac{\frac{1}{2}}{\frac{\sqrt{15}}{2}}$=$\frac{\sqrt{15}}{15}$.故结论II正确.
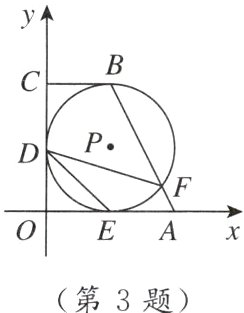
3. 新考法 等角代换法 如图,在平面直角坐标系中,四边形OABC是直角梯形,BC//OA,⊙P分别与OA,OC,BC相切于点E,D,B,与AB交于点F,连接DE,DF. 已知A(2,0),B(1,2),则tan∠FDE的值为______.

答案:
$\frac{1}{2}$ [点拨]如图,连接PB,PE.
∵⊙P分别与OA,BC相切于点E,B,
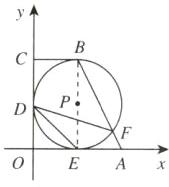
∴PB⊥BC,PE⊥OA.又
∵BC//OA,
∴B,P,E三点在同一条直线上.
∵A(2,0),B(1,2),
∴AE=1,BE=2.
∴tan∠ABE=$\frac{AE}{BE}$=$\frac{1}{2}$.
又
∵∠EDF=∠ABE,
∴tan∠FDE=tan∠ABE=$\frac{1}{2}$.
$\frac{1}{2}$ [点拨]如图,连接PB,PE.
∵⊙P分别与OA,BC相切于点E,B,

∴PB⊥BC,PE⊥OA.又
∵BC//OA,
∴B,P,E三点在同一条直线上.
∵A(2,0),B(1,2),
∴AE=1,BE=2.
∴tan∠ABE=$\frac{AE}{BE}$=$\frac{1}{2}$.
又
∵∠EDF=∠ABE,
∴tan∠FDE=tan∠ABE=$\frac{1}{2}$.
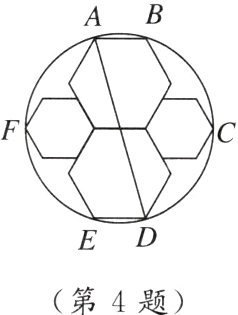
4. 如图,已知四个正六边形摆放在圆中,顶点A,B,C,D,E,F在圆上,其中上下两个大一点的正六边形的边长均为a,左右两个正六边形的边长均为b.
(1)tan∠ADE = ______;
(2)若b = 3,则a = ______.
(1)tan∠ADE = ______;
(2)若b = 3,则a = ______.

答案:
(1)$2\sqrt{3}$
(2)$\sqrt{13}+1$ [点拨]
(1)如图,设AD交MN 于点O,由对称性可知,点O即为圆心,连接AE,则AE过点N,且AE⊥DE,过点P作PQ⊥AE,垂足为Q,
在Rt△APQ中,∠APQ=$\frac{120^{\circ}}{2}$=60°,AP = a,
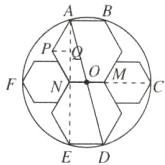
∴易得AQ=$\frac{\sqrt{3}}{2}$AP=$\frac{\sqrt{3}}{2}$a.
∴易得AE=4AQ=$2\sqrt{3}$a.
在Rt△ADE中,tan∠ADE=$\frac{AE}{DE}$=$\frac{2\sqrt{3}a}{a}$=$2\sqrt{3}$
(2)如图,连接MC,易知点O,M,C在同一条直线上.
在Rt△AON中,易知AN=$\sqrt{3}$a,ON=$\frac{1}{2}$MN=$\frac{1}{2}$a,
∴OA=$\sqrt{AN^{2}+ON^{2}}$=$\frac{\sqrt{13}}{2}$a.
易知OC=OM+MC=$\frac{1}{2}$a+2b,OA=OC,
∴$\frac{\sqrt{13}}{2}$a=$\frac{1}{2}$a+2b,即$\frac{\sqrt{13}}{2}$a=$\frac{1}{2}$a+6,
解得a=$\sqrt{13}+1$.
(1)$2\sqrt{3}$
(2)$\sqrt{13}+1$ [点拨]
(1)如图,设AD交MN 于点O,由对称性可知,点O即为圆心,连接AE,则AE过点N,且AE⊥DE,过点P作PQ⊥AE,垂足为Q,
在Rt△APQ中,∠APQ=$\frac{120^{\circ}}{2}$=60°,AP = a,

∴易得AQ=$\frac{\sqrt{3}}{2}$AP=$\frac{\sqrt{3}}{2}$a.
∴易得AE=4AQ=$2\sqrt{3}$a.
在Rt△ADE中,tan∠ADE=$\frac{AE}{DE}$=$\frac{2\sqrt{3}a}{a}$=$2\sqrt{3}$
(2)如图,连接MC,易知点O,M,C在同一条直线上.
在Rt△AON中,易知AN=$\sqrt{3}$a,ON=$\frac{1}{2}$MN=$\frac{1}{2}$a,
∴OA=$\sqrt{AN^{2}+ON^{2}}$=$\frac{\sqrt{13}}{2}$a.
易知OC=OM+MC=$\frac{1}{2}$a+2b,OA=OC,
∴$\frac{\sqrt{13}}{2}$a=$\frac{1}{2}$a+2b,即$\frac{\sqrt{13}}{2}$a=$\frac{1}{2}$a+6,
解得a=$\sqrt{13}+1$.
5. 如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧AB,使点B在点O的右下方,且tan∠AOB = $\frac{4}{3}$. 在优弧AB上任取一点P,且能过点P作直线l//OB交数轴于点Q,设Q点在数轴上对应的数为x,连接OP.
(1)若优弧AB上一段$\overset{\frown}{AP}$的长为13π,则∠AOP的度数为______,x的值为______;
(2)x的最小值为______,此时直线l与优弧AB所在圆的位置关系为______.

(1)若优弧AB上一段$\overset{\frown}{AP}$的长为13π,则∠AOP的度数为______,x的值为______;
(2)x的最小值为______,此时直线l与优弧AB所在圆的位置关系为______.

答案:
(1)$90^{\circ}$;$\frac{39}{2}$
(2)−32.5;相切 [点拨]
(1)设∠AOP=n°,由$\frac{n\cdot\pi\times26}{180}$=13π,解得n=90,
∴∠AOP=90°.
∵PQ//OB,
∴∠PQO=∠BOQ,
∴tan∠PQO=tan∠QOB=$\frac{4}{3}$=$\frac{OP}{OQ}$.
∴$\frac{4}{3}$=$\frac{26}{OQ}$
∴OQ=$\frac{39}{2}$.
∴x=$\frac{39}{2}$.
(2)如图,当直线PQ与⊙O相切时,x的值最小,
∵PQ与⊙O相切,
∴∠OPQ=90°
∵PQ//OB,
∴∠PQO=∠AOB.
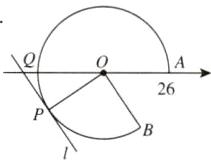
∴tan∠PQO=$\frac{OP}{PQ}$=$\frac{4}{3}$
∴PQ=19.5.
由勾股定理得OQ=32.5.
∴x=−32.5.
(1)$90^{\circ}$;$\frac{39}{2}$
(2)−32.5;相切 [点拨]
(1)设∠AOP=n°,由$\frac{n\cdot\pi\times26}{180}$=13π,解得n=90,
∴∠AOP=90°.
∵PQ//OB,
∴∠PQO=∠BOQ,
∴tan∠PQO=tan∠QOB=$\frac{4}{3}$=$\frac{OP}{OQ}$.
∴$\frac{4}{3}$=$\frac{26}{OQ}$
∴OQ=$\frac{39}{2}$.
∴x=$\frac{39}{2}$.
(2)如图,当直线PQ与⊙O相切时,x的值最小,
∵PQ与⊙O相切,
∴∠OPQ=90°
∵PQ//OB,
∴∠PQO=∠AOB.

∴tan∠PQO=$\frac{OP}{PQ}$=$\frac{4}{3}$
∴PQ=19.5.
由勾股定理得OQ=32.5.
∴x=−32.5.
6. 新考法 分类讨论法 如图,在△ABC中,∠ACB = 90°,sin A = $\frac{3}{5}$,AC = 8,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A'B'上的动点,以点P为圆心,PA'长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为______.


答案:
$\frac{40}{9}$或$\frac{28}{5}$ [点拨]
∵∠ACB=90°,sinA=$\frac{3}{5}$,
∴可设BC=3x,则AB=5x,
在Rt△ABC中,由勾股定理,得AB²=AC²+BC²,
即$(5x)^{2}$=8²+(3x)²,解得x=2(负值已舍去).
∴AB=10,BC=6.
∴cosA=$\frac{AC}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
①若⊙P与AC相切,如图①.
设切点为M,连接PM,则PM⊥AC,且PM=PA′,
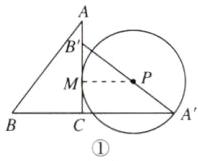
∵PM⊥AC,易知A′C⊥AC,
∴PM//A′C,
∴∠B′PM=∠A′.
由旋转的性质可知∠A′=∠A,
∴∠B′PM=∠A.
∴cos∠B′PM=$\frac{PM}{B′P}$=cosA=$\frac{4}{5}$.
设PM=4a,则PA′=4a,B′P=5a.
∵A′B′=AB,
∴PA′+B′P=A′B′=AB,即4a+5a=10,
解得a=$\frac{10}{9}$,
∴PA′=4a=$\frac{40}{9}$.
∴此时⊙P的半径为$\frac{40}{9}$.
②若⊙P与AB相切,延长PB′交AB于点N,如图②.
∵∠A′+∠B=∠A+∠B=90°,
∴∠A′NB=90°,
即N为AB与⊙P的切点,
∵A′B=BC+A′C=BC+AC=14,
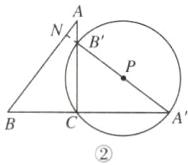
∴A′N=A′B·cosA=14×$\frac{4}{5}$=$\frac{56}{5}$.
∴PA′=$\frac{1}{2}$A′N=$\frac{28}{5}$.
由题意易知⊙P与BC不可能相切.
综上,⊙P的半径为$\frac{40}{9}$或$\frac{28}{5}$.
$\frac{40}{9}$或$\frac{28}{5}$ [点拨]
∵∠ACB=90°,sinA=$\frac{3}{5}$,
∴可设BC=3x,则AB=5x,
在Rt△ABC中,由勾股定理,得AB²=AC²+BC²,
即$(5x)^{2}$=8²+(3x)²,解得x=2(负值已舍去).
∴AB=10,BC=6.
∴cosA=$\frac{AC}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
①若⊙P与AC相切,如图①.
设切点为M,连接PM,则PM⊥AC,且PM=PA′,

∵PM⊥AC,易知A′C⊥AC,
∴PM//A′C,
∴∠B′PM=∠A′.
由旋转的性质可知∠A′=∠A,
∴∠B′PM=∠A.
∴cos∠B′PM=$\frac{PM}{B′P}$=cosA=$\frac{4}{5}$.
设PM=4a,则PA′=4a,B′P=5a.
∵A′B′=AB,
∴PA′+B′P=A′B′=AB,即4a+5a=10,
解得a=$\frac{10}{9}$,
∴PA′=4a=$\frac{40}{9}$.
∴此时⊙P的半径为$\frac{40}{9}$.
②若⊙P与AB相切,延长PB′交AB于点N,如图②.
∵∠A′+∠B=∠A+∠B=90°,
∴∠A′NB=90°,
即N为AB与⊙P的切点,
∵A′B=BC+A′C=BC+AC=14,

∴A′N=A′B·cosA=14×$\frac{4}{5}$=$\frac{56}{5}$.
∴PA′=$\frac{1}{2}$A′N=$\frac{28}{5}$.
由题意易知⊙P与BC不可能相切.
综上,⊙P的半径为$\frac{40}{9}$或$\frac{28}{5}$.
7. 如图,AB是半圆O的直径,EB,EC分别与半圆O相切于点B,C,连接AC并延长,与BE的延长线交于点D.
(1)求证:EB = ED;
(2)若AC = 8,cos D = $\frac{3}{5}$,请直接写出AB的长.

(1)求证:EB = ED;
(2)若AC = 8,cos D = $\frac{3}{5}$,请直接写出AB的长.

答案:
(1)[证明]如图,连接BC.
∵EB,EC分别与半圆O相切于点B,C,
∴EC=EB.
∴∠ECB=∠EBC;
∵AB是半圆O直径,
∴∠ACB=90°,
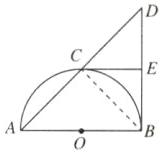
∴∠DCB=90°,
即∠DCE+∠ECB=90°.
∴∠D+∠DBC=90°.
∴∠D=∠DCE.
∴DE=CE.
∴EB=ED.
(2)[解]AB的长为10.
(1)[证明]如图,连接BC.
∵EB,EC分别与半圆O相切于点B,C,
∴EC=EB.
∴∠ECB=∠EBC;
∵AB是半圆O直径,
∴∠ACB=90°,

∴∠DCB=90°,
即∠DCE+∠ECB=90°.
∴∠D+∠DBC=90°.
∴∠D=∠DCE.
∴DE=CE.
∴EB=ED.
(2)[解]AB的长为10.
查看更多完整答案,请扫码查看


