第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. [2024宿州模拟] 对于二次函数$y=(x + 3)^2$,下列说法不正确的是 ( )
A. 图像的开口向上
B. 图像的对称轴是直线$x = - 3$
C. 图像的顶点坐标为$(-3,0)$
D. 当$x < - 3$时,$y$随$x$的增大而增大
A. 图像的开口向上
B. 图像的对称轴是直线$x = - 3$
C. 图像的顶点坐标为$(-3,0)$
D. 当$x < - 3$时,$y$随$x$的增大而增大
答案:
D
2. 若抛物线$y=\frac{2}{3}(x - 1)^2 + c$经过$(-2,y_1)$,$(0,y_2)$,$(\frac{5}{2},y_3)$三点,则$y_1$,$y_2$,$y_3$的大小关系为 ( )
A. $y_1>y_2>y_3$
B. $y_2>y_3>y_1$
C. $y_3>y_1>y_2$
D. $y_1>y_3>y_2$
A. $y_1>y_2>y_3$
B. $y_2>y_3>y_1$
C. $y_3>y_1>y_2$
D. $y_1>y_3>y_2$
答案:
D
3. [2024滨州] 将抛物线$y = - x^2$先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为________.
答案:
(1,2)
4. 已知抛物线$y = a(x + 1)^2 + 2$过点$(0,y_1)$,$(3,y_2)$,若$y_1>y_2$,则$a$的取值范围是________.
答案:
$a<0$
5. [新视角 动手操作题] 已知二次函数$y = -(x + 2)^2$.
(1)完成下表,并在如图所示的平面直角坐标系中画出该函数的图像;
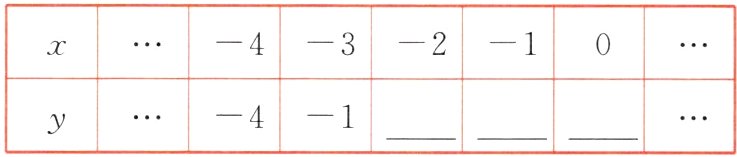
(2)该函数图像的顶点坐标为________;
(3)结合图像,请直接写出当$x$取何值时,$y$随$x$的增大而减小.

(1)完成下表,并在如图所示的平面直角坐标系中画出该函数的图像;

(2)该函数图像的顶点坐标为________;
(3)结合图像,请直接写出当$x$取何值时,$y$随$x$的增大而减小.

答案:
【解】
(1)0;-1;-4
函数图像如图所示.

(2)(-2,0)
(3)当$x>-2$时,$y$随$x$的增大而减小.
【解】
(1)0;-1;-4
函数图像如图所示.

(2)(-2,0)
(3)当$x>-2$时,$y$随$x$的增大而减小.
6. [易错题] 在平面直角坐标系中,如果抛物线$y = 3x^2$不动,把$x$轴、$y$轴分别向上、向右平移5个单位长度,那么在新坐标系中此抛物线的表达式是 ( )
A. $y = 3(x - 5)^2 + 5$
B. $y = 3(x - 5)^2 - 5$
C. $y = 3(x + 5)^2 + 5$
D. $y = 3(x + 5)^2 - 5$
A. $y = 3(x - 5)^2 + 5$
B. $y = 3(x - 5)^2 - 5$
C. $y = 3(x + 5)^2 + 5$
D. $y = 3(x + 5)^2 - 5$
答案:
D 【点拨】抛物线$y = 3x^2$的顶点坐标为(0,0),把$x$轴、$y$轴分别向上、向右平移5个单位长度后,易知顶点的坐标变为(-5,-5),所以在新坐标系中此抛物线的表达式为$y = 3(x + 5)^2 - 5$.
7. [易错题] 已知$a(a < 0)$,$h(0 < h < 10)$,$k$为常数,且二次函数$y = a(x - h)^2 + k$的图像经过$(0,5)$,$(10,8)$两点. 对于结论Ⅰ和Ⅱ,下列判断正确的是 ( )
结论Ⅰ:$h$的值可能为5;
结论Ⅱ:点$P(m,n)$在二次函数的图像上,若$n = 8$,则满足条件的点$P$有两个.
A. Ⅰ和Ⅱ都对
B. Ⅰ和Ⅱ都不对
C. Ⅰ不对,Ⅱ对
D. Ⅰ对,Ⅱ不对
结论Ⅰ:$h$的值可能为5;
结论Ⅱ:点$P(m,n)$在二次函数的图像上,若$n = 8$,则满足条件的点$P$有两个.
A. Ⅰ和Ⅱ都对
B. Ⅰ和Ⅱ都不对
C. Ⅰ不对,Ⅱ对
D. Ⅰ对,Ⅱ不对
答案:
C 【点拨】$\because y = a(x - h)^2 + k$,$\therefore$该函数图像的对称轴为直线$x = h$.$\because a<0$,$\therefore$该函数图像的开口向下.$\because$二次函数的图像经过(0,5),(10,8)两点,$0 < h < 10$,$\therefore$易得$5 < h < 10$,$\therefore$结论Ⅰ不对.
由上述可知点(10,8)不是抛物线的顶点,$\therefore$函数的最大值大于8.
$\therefore$易得满足条件的点$P$有两个,故结论Ⅱ对. 故选C.
由上述可知点(10,8)不是抛物线的顶点,$\therefore$函数的最大值大于8.
$\therefore$易得满足条件的点$P$有两个,故结论Ⅱ对. 故选C.
8. [2024邯郸期末] 已知二次函数$y=(x - h)^2 + 1$($h$为常数),在自变量$x$的值满足$1\leqslant x\leqslant 3$的情况下,与其对应的函数值$y$的最小值为5,则$h$的值为 ( )
A. 1或 - 5
B. - 1或5
C. 1或 - 3
D. 1或3
A. 1或 - 5
B. - 1或5
C. 1或 - 3
D. 1或3
答案:
B 【点拨】对于$y=(x - h)^2 + 1$,当$x>h$时,$y$随$x$的增大而增大,当$x < h$时,$y$随$x$的增大而减小.
$\therefore$可分情况讨论:①若$h < 1$,则当$x = 1$时,$y$取得最小值5,可得$(1 - h)^2 + 1 = 5$,解得$h = - 1$或$h = 3$(舍去).
②若$h>3$,则当$x = 3$时,$y$取得最小值5,可得$(3 - h)^2 + 1 = 5$,解得$h = 5$或$h = 1$(舍去).
③若$1\leqslant h\leqslant 3$,则当$x = h$时,$y$取得最小值,此时$y = 1\neq5$,$\therefore$此情况不符合题意.
综上,$h$的值为-1或5.
点技巧 当二次函数的自变量受到限制时,它的最值不一定为图像顶点的纵坐标,这时,我们要通过分类讨论并结合函数的增减性进行判断.
$\therefore$可分情况讨论:①若$h < 1$,则当$x = 1$时,$y$取得最小值5,可得$(1 - h)^2 + 1 = 5$,解得$h = - 1$或$h = 3$(舍去).
②若$h>3$,则当$x = 3$时,$y$取得最小值5,可得$(3 - h)^2 + 1 = 5$,解得$h = 5$或$h = 1$(舍去).
③若$1\leqslant h\leqslant 3$,则当$x = h$时,$y$取得最小值,此时$y = 1\neq5$,$\therefore$此情况不符合题意.
综上,$h$的值为-1或5.
点技巧 当二次函数的自变量受到限制时,它的最值不一定为图像顶点的纵坐标,这时,我们要通过分类讨论并结合函数的增减性进行判断.
9. 平面直角坐标系上有两个二次函数的图像,其顶点$M$,$N$皆在$x$轴上,且有一平行于$x$轴的直线与两图像分别相交于$A$,$C$,$B$,$D$四点,各点位置如图所示,若$AB = 12$,$BC = 4$,$CD = 6$,则$MN$的长是 ( )
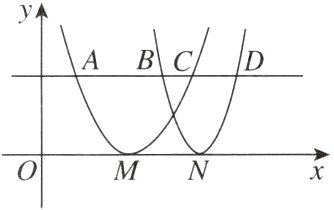
A. 8
B. 9
C. 10
D. 11

A. 8
B. 9
C. 10
D. 11
答案:
B 【点拨】设$A(x,y)$,易得$B(x + 12,y)$,$C(x + 16,y)$,$D(x + 22,y)$,
$\therefore M$的横坐标为$\frac{x + x + 16}{2}=x + 8$,$N$的横坐标为$\frac{x + 12 + x + 22}{2}=x + 17$.$\therefore MN=x + 17-(x + 8)=9$.
$\therefore M$的横坐标为$\frac{x + x + 16}{2}=x + 8$,$N$的横坐标为$\frac{x + 12 + x + 22}{2}=x + 17$.$\therefore MN=x + 17-(x + 8)=9$.
查看更多完整答案,请扫码查看


