第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
8. 如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD分别交AM,BN于点D,C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)若AD = 4,BC = 9,求⊙O的半径R.

(1)求证:CD是⊙O的切线;
(2)若AD = 4,BC = 9,求⊙O的半径R.

答案:
(1)【证明】过点O作OE⊥CD于点E.
∵AM切⊙O于点A,
∴OA⊥AD.
又
∵DO平分∠ADC,
∴OE = OA.
∵OA是⊙O的半径,
∴OE是⊙O的半径.
∴CD是⊙O的切线.
(2)【解】过点D作DF⊥BC于点F.
∵AM,BN分别切⊙O于点A,B,
∴AB⊥AD,AB⊥BC.
∴四边形ABFD是矩形.
∴BF = AD = 4,AB = DF.
∵BC = 9,
∴FC = 9 - 4 = 5.
∵AM,BN,DC分别切⊙O于点A,B,E,
∴DA = DE,CB = CE.
∴DC = DE + CE = AD + BC = 4 + 9 = 13.
在Rt△DFC中,DC² = DF² + FC²,
∴DF = $\sqrt{DC² - FC²}$ = $\sqrt{13² - 5²}$ = 12.
∴AB = 12,
∴⊙O的半径R是6.
(1)【证明】过点O作OE⊥CD于点E.
∵AM切⊙O于点A,
∴OA⊥AD.
又
∵DO平分∠ADC,
∴OE = OA.
∵OA是⊙O的半径,
∴OE是⊙O的半径.
∴CD是⊙O的切线.
(2)【解】过点D作DF⊥BC于点F.
∵AM,BN分别切⊙O于点A,B,
∴AB⊥AD,AB⊥BC.
∴四边形ABFD是矩形.
∴BF = AD = 4,AB = DF.
∵BC = 9,
∴FC = 9 - 4 = 5.
∵AM,BN,DC分别切⊙O于点A,B,E,
∴DA = DE,CB = CE.
∴DC = DE + CE = AD + BC = 4 + 9 = 13.
在Rt△DFC中,DC² = DF² + FC²,
∴DF = $\sqrt{DC² - FC²}$ = $\sqrt{13² - 5²}$ = 12.
∴AB = 12,
∴⊙O的半径R是6.
9. 如图①,在四边形ABCD中,∠A = ∠B = 90°,AD + BC = CD,以AB为直径作⊙O.
(1)求证:CD与⊙O相切;
(2)如图②,若CD切⊙O于点E,连接OE,AC,OE与AC交于点F,若FC = 2AF,求BC/AD的值.
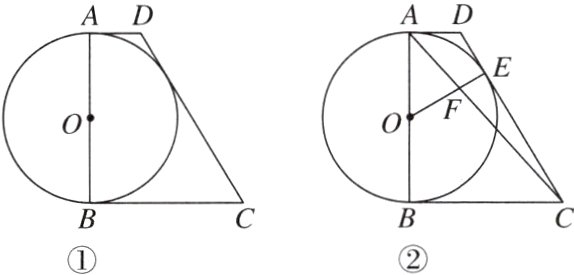
(1)求证:CD与⊙O相切;
(2)如图②,若CD切⊙O于点E,连接OE,AC,OE与AC交于点F,若FC = 2AF,求BC/AD的值.

答案:
(1)【证明】如图①,连接CO并延长,与DA的延长线交于点H,过点O作OE⊥CD于点E,
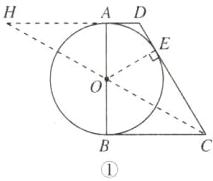
易知∠OAH = ∠ABC = 90°,
又
∵∠AOH = ∠BOC,AO = BO,
∴△AOH≌△BOC(ASA).
∴AH = BC,HO = CO.
∵AD + BC = CD,
∴AH + AD = HD = CD.
∴∠H = ∠DCH.
又
∵∠OAH = ∠OEC = 90°,HO = CO,
∴△AHO≌△ECO(AAS).
∴AO = OE.
∴OE为⊙O的半径.
∵OE⊥CD.
∴CD与⊙O相切.
(2)【解】如图②,作CT⊥BC交OE的延长线于点T,连接AT.则∠TCB = 90°.
∴∠B + ∠TCB = 180°,
∴AB//CT.
∴易得△AFO∽△CFT.
∴$\frac{CF}{AF}$ = $\frac{CT}{AO}$ = 2.
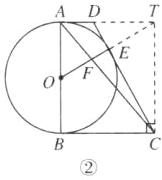
∴CT = 2OA.
∵AB = 2OA,
∴CT = AB.
∴四边形ABCT是平行四边形.
∵∠B = 90°,
∴四边形ABCT是矩形.
∴∠ATC = 90°,AT//BC,AT = BC.
易知AD//BC,
∴A,D,T三点共线.
∵CD是⊙O的切线,∠A = ∠B = 90°,
∴OT⊥CD,DA = DE,CB = CE.
∴∠DET = ∠DTC = 90°.
又
∵∠TDE = ∠CDT,
∴△DTE∽△DCT.
∴$\frac{TD}{CD}$ = $\frac{DE}{DT}$.
∴TD² = DE·DC.
设AD = DE = x,CB = CE = AT = y,则DT = AT - AD = y - x,CD = DE + CE = x + y.
∴(y - x)² = x(x + y),整理,得y² = 3xy,
∵y≠0,
∴y = 3x.
∴$\frac{BC}{AD}$ = $\frac{y}{x}$ = 3.
(1)【证明】如图①,连接CO并延长,与DA的延长线交于点H,过点O作OE⊥CD于点E,

易知∠OAH = ∠ABC = 90°,
又
∵∠AOH = ∠BOC,AO = BO,
∴△AOH≌△BOC(ASA).
∴AH = BC,HO = CO.
∵AD + BC = CD,
∴AH + AD = HD = CD.
∴∠H = ∠DCH.
又
∵∠OAH = ∠OEC = 90°,HO = CO,
∴△AHO≌△ECO(AAS).
∴AO = OE.
∴OE为⊙O的半径.
∵OE⊥CD.
∴CD与⊙O相切.
(2)【解】如图②,作CT⊥BC交OE的延长线于点T,连接AT.则∠TCB = 90°.
∴∠B + ∠TCB = 180°,
∴AB//CT.
∴易得△AFO∽△CFT.
∴$\frac{CF}{AF}$ = $\frac{CT}{AO}$ = 2.

∴CT = 2OA.
∵AB = 2OA,
∴CT = AB.
∴四边形ABCT是平行四边形.
∵∠B = 90°,
∴四边形ABCT是矩形.
∴∠ATC = 90°,AT//BC,AT = BC.
易知AD//BC,
∴A,D,T三点共线.
∵CD是⊙O的切线,∠A = ∠B = 90°,
∴OT⊥CD,DA = DE,CB = CE.
∴∠DET = ∠DTC = 90°.
又
∵∠TDE = ∠CDT,
∴△DTE∽△DCT.
∴$\frac{TD}{CD}$ = $\frac{DE}{DT}$.
∴TD² = DE·DC.
设AD = DE = x,CB = CE = AT = y,则DT = AT - AD = y - x,CD = DE + CE = x + y.
∴(y - x)² = x(x + y),整理,得y² = 3xy,
∵y≠0,
∴y = 3x.
∴$\frac{BC}{AD}$ = $\frac{y}{x}$ = 3.
查看更多完整答案,请扫码查看


