第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 如图,如果⊙O的半径为5,那么图中到圆心O的距离为7的点可能是( )

A. P点 B. Q点 C. M点 D. N点

A. P点 B. Q点 C. M点 D. N点
答案:
D
2. [2024保定期末] 在Rt△ABC中,∠ACB = 90°,AC = 6,AB = 10,以点C为圆心,BC长为半径作⊙C,则点A与⊙C的位置关系是( )
A. 点A在⊙C内 B. 点A在⊙C上
C. 点A在⊙C外 D. 无法确定
A. 点A在⊙C内 B. 点A在⊙C上
C. 点A在⊙C外 D. 无法确定
答案:
A
3. 若⊙P的半径为4,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )
A. 点O在⊙P内 B. 点O在⊙P上
C. 点O在⊙P外 D. 无法确定
A. 点O在⊙P内 B. 点O在⊙P上
C. 点O在⊙P外 D. 无法确定
答案:
C
4. 在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2. 下列说法中不正确的是( )
A. 当a = 1时,点B在⊙A上
B. 当2<a<3时,点B在⊙A内
C. 当a<5时,点B在⊙A内
D. 当a>5时,点B在⊙A外
A. 当a = 1时,点B在⊙A上
B. 当2<a<3时,点B在⊙A内
C. 当a<5时,点B在⊙A内
D. 当a>5时,点B在⊙A外
答案:
C
5. 母题教材P4习题A组T2 已知矩形ABCD的边AB = 6,BC = 8,以点B为圆心作圆,使A,C,D三点中至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( )
A. r>6 B. 6<r<8
C. 6<r<10 D. 6<r<8或8<r<10
A. r>6 B. 6<r<8
C. 6<r<10 D. 6<r<8或8<r<10
答案:
C
6. 新趋势 学科内综合 已知⊙O的半径是4,点P到圆心O的距离d为方程x²-4x-5 = 0的一个根,则点P与⊙O的位置关系是__________.
答案:
点P在⊙O外
7. 母题教材P3例 如图,在△ABC中,∠ACB = 90°,AC = 4,BC = 5,AB的中点为点M.
(1)以点C为圆心,4为半径作⊙C,则点A,B,M分别与⊙C有怎样的位置关系?
(2)以点C为圆心作⊙C,使A,B,M三点中至少有一点在⊙C内,且至少有一点在⊙C外,求⊙C的半径r的取值范围.
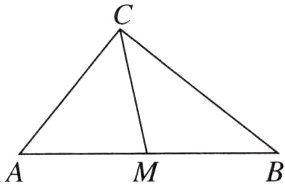
(1)以点C为圆心,4为半径作⊙C,则点A,B,M分别与⊙C有怎样的位置关系?
(2)以点C为圆心作⊙C,使A,B,M三点中至少有一点在⊙C内,且至少有一点在⊙C外,求⊙C的半径r的取值范围.

答案:
【解】
(1)
∵在△ABC中,∠ACB = 90°,AC = 4,BC = 5,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{16 + 25}=\sqrt{41}$.
∵AB的中点为点M,
∴CM = $\frac{1}{2}AB=\frac{\sqrt{41}}{2}$.
由题知⊙C的半径为4.
∵AC = 4,
∴点A在⊙C上.
∵CM = $\frac{\sqrt{41}}{2}<4$,
∴点M在⊙C内.
∵BC = 5>4,
∴点B在⊙C外.
(2)以点C为圆心作⊙C,使A,B,M三点中至少有一点在⊙C内时,r>$\frac{\sqrt{41}}{2}$,
至少有一点在⊙C外时,r<5,
故⊙C的半径r的取值范围为$\frac{\sqrt{41}}{2}<r<5$.
(1)
∵在△ABC中,∠ACB = 90°,AC = 4,BC = 5,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{16 + 25}=\sqrt{41}$.
∵AB的中点为点M,
∴CM = $\frac{1}{2}AB=\frac{\sqrt{41}}{2}$.
由题知⊙C的半径为4.
∵AC = 4,
∴点A在⊙C上.
∵CM = $\frac{\sqrt{41}}{2}<4$,
∴点M在⊙C内.
∵BC = 5>4,
∴点B在⊙C外.
(2)以点C为圆心作⊙C,使A,B,M三点中至少有一点在⊙C内时,r>$\frac{\sqrt{41}}{2}$,
至少有一点在⊙C外时,r<5,
故⊙C的半径r的取值范围为$\frac{\sqrt{41}}{2}<r<5$.
8. [2024杭州拱墅区期末] 如图,在Rt△ABC中,∠B = 90°,AB = 4,BC = 7,点D在边BC上,且BD = 3,连接AD. 以点D为圆心,r为半径画圆,若点A,B,C中只有1个点在圆内,则r的值可能为( )
A. 3
B. 4
C. 5
D. 6
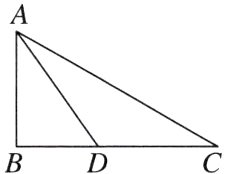
A. 3
B. 4
C. 5
D. 6

答案:
B 【点拨】在Rt△ABD中,∠B = 90°,AB = 4,BD = 3,
∴AD = $\sqrt{AB^{2}+BD^{2}}=\sqrt{4^{2}+3^{2}} = 5$.
∵BC = 7,
∴CD = BC - BD = 7 - 3 = 4.
∵以点D为圆心,r为半径画圆,点A,B,C中只有1个点在圆内,
∴r的取值范围是3<r≤4,
∴r的值可能为4.
∴AD = $\sqrt{AB^{2}+BD^{2}}=\sqrt{4^{2}+3^{2}} = 5$.
∵BC = 7,
∴CD = BC - BD = 7 - 3 = 4.
∵以点D为圆心,r为半径画圆,点A,B,C中只有1个点在圆内,
∴r的取值范围是3<r≤4,
∴r的值可能为4.
9. [2024宁波模拟] 在△ABC中,∠A = 60°,以BC为直径画圆,则点A( )
A. 一定在圆外
B. 一定在圆上
C. 一定在圆内
D. 在圆外或圆内,但一定不在圆上
A. 一定在圆外
B. 一定在圆上
C. 一定在圆内
D. 在圆外或圆内,但一定不在圆上
答案:
A 【点拨】如图,BC为圆的直径,

当点A'在圆上时,∠BA'C = 90°,因为∠A = 60°,所以点A一定在圆外.
A 【点拨】如图,BC为圆的直径,

当点A'在圆上时,∠BA'C = 90°,因为∠A = 60°,所以点A一定在圆外.
查看更多完整答案,请扫码查看


