《2025年综合应用创新题典中点九年级数学下册冀教版》

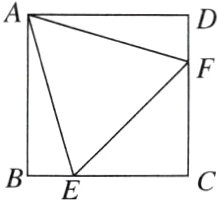
11. 如图，在正方形ABCD中，AB = 4，E为BC上一点，F为CD上一点，且AE = AF. 设△AEF的面积为y，CE = x.
(1)求y关于x的函数表达式；
(2)当△AEF为正三角形时，求△AEF的面积.
　　　　　　　　　　　　　　

答案： 【解】
(1)
∵四边形ABCD为正方形，
　
∴∠B = ∠C = ∠D = 90°,AD = BC = CD = AB = 4.
　　又
∵AE = AF,
∴Rt△ABE≌Rt△ADF(HL).
　
∴$S_△ABE = S_△ADF,BE = DF.　　$
∴BC - BE = CD - DF,即CE = CF.
　
∵CE = x,
∴CF = x,BE = 4 - x.
　
∴$S_△ABE = 1/2AB·BE = 1/2×4×(4 - x) = 8 - 2x,S_△CEF = 1/2CE·CF = 1/2x².　　$
∴y = S_正方形$ABCD - 2S_△ABE - S_△CEF = 4² - 2(8 - 2x) - 1/2x² = -1/2x² + 4x(0 $＜ x ＜ 4).
(2)当△AEF为正三角形时,AE = EF,
　
∴AE² = EF²,
　
∴AB² + BE² = CE² + CF²,即16 + (4 - x)² = 2x²,
　　整理,得x² + 8x - 32 = 0,解得x = -4±4√3.
　
∵x ＞ 0,
∴x = 4√3 - 4.
∴y = -1/2x² + 4x = -1/2×(4√3 - 4)² + 4×(4√3 - 4) = 32√3 - 48.
　
∴当△AEF为正三角形时,△AEF的面积为32√3 - 48.

12. 情境题 社会热点 [2024·阜阳期末] 某市公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定. 某头盔经销商统计了某品牌头盔4月份到6月份的销售量，该品牌头盔4月份销售150个，6月份销售216个，且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔4月份到6月份销售量的月增长率；
(2)若该品牌头盔的进价为30元/个，经测算在市场中，当售价为40元/个时，月销售量为600个，若在此基础上每个头盔的售价每上涨1元，则月销售量将减少10个.
①设该品牌头盔的实际售价为a元/个，每月获得的利润为y元，列出y与a的函数关系式.
②为使月销售利润达到10 000元，而且尽可能让顾客得到实惠，则该品牌头盔的实际售价应定为多少？

答案： 【解】
(1)设该品牌头盔4月份到6月份销售量的月增长率为x,
　　根据题意,得150(1 + x)² = 216,
　　解得x₁ = 0.2 = 20%,x₂ = -2.2(不合题意,舍去).
　
∴该品牌头盔4月份到6月份销售量的月增长率为20%.
(2)①由题意,得y = (a - 30)[600 - (a - 40)×10] = -10a² + 1300a - 30000,
　
∴y与a的函数关系式为y = -10a² + 1300a - 30000.
②由题意,得 - 10a² + 1300a - 30000 = 10000,解得a₁ = 50,a₂ = 80.
　
∵要尽可能让顾客得到实惠,
∴a = 50.
　
∴该品牌头盔的实际售价应定为50元/个.

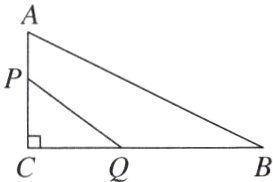
13. 新视角 动点探究题 如图，在Rt△ABC中，∠C = 90°，AC = 12 mm，BC = 24 mm，动点P从点A开始沿边AC向C以2 mm/s的速度运动，同时动点Q从点C开始沿边CB向B以4 mm/s的速度运动，设P，Q的运动时间为t s.
(1)已知△PCQ的面积为S₁ mm²，写出S₁与t的函数表达式及t的取值范围；
(2)已知四边形APQB的面积为S₂ mm²，请写出S₂与t的函数表达式.
　　　　　　　　　　　　　

答案： 【解】
(1)由题意得PC = (12 - 2t)mm,CQ = 4t mm.
　
∴S₁ = 1/2×(12 - 2t)×4t = -4t² + 24t.
　
∵{0 ＜ 4t ＜ 24, 0 ＜ 12 - 2t ＜ 12},
∴$0 ＜ t ＜ 6.(2)S₂ = S_△ABC - S₁ = 1/2×24×12 - (-4t² + 24t) = 4t² - 24t + 144(0 ＜ t ＜ 6).$点技巧 在解决动点问题时,要明确问题中点的运动方向和速度,根据线段之间的关系列出函数表达式,并注意题目中自变量的取值范围.