第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
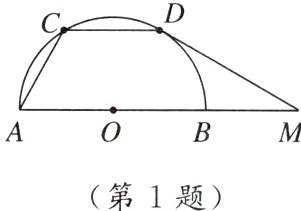
1. [2024邢台校级月考]如图,已知AB是半圆O的直径,点C,D将弧AB分成相等的三段弧,点M在AB的延长线上,连接MD.对于下列两个结论,判断正确的是 ( )
结论Ⅰ:若∠OMD = 30°,则MD为半圆O的切线;
结论Ⅱ:连接AC,CD,则∠ACD = 130°.
A. Ⅰ和Ⅱ都对
B. Ⅰ对Ⅱ错
C. Ⅰ错Ⅱ对
D. Ⅰ和Ⅱ都错
结论Ⅰ:若∠OMD = 30°,则MD为半圆O的切线;
结论Ⅱ:连接AC,CD,则∠ACD = 130°.

A. Ⅰ和Ⅱ都对
B. Ⅰ对Ⅱ错
C. Ⅰ错Ⅱ对
D. Ⅰ和Ⅱ都错
答案:
B
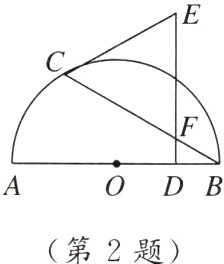
2. 如图,AB是半圆O的直径,点C在半圆上(不与点A,B重合),DE⊥AB于点D,交BC于点F,下列条件中能判断CE是半圆O的切线的是 ( )
A. ∠E = ∠CFE
B. ∠E = ∠ECF
C. ∠ECF = ∠EFC
D. ∠ECF = 60°

A. ∠E = ∠CFE
B. ∠E = ∠ECF
C. ∠ECF = ∠EFC
D. ∠ECF = 60°
答案:
C
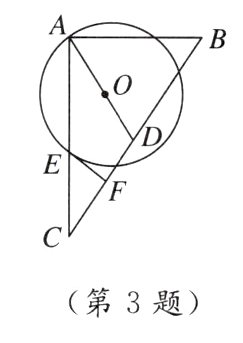
3. [新视角 条件开放题]如图,在△ABC中,∠BAC = 90°,D为BC的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于另一点E,要使EF是⊙O的切线,需要添加的一个条件是________(写一个条件即可).

答案:
EF⊥BC(答案不唯一)
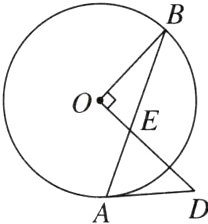
4. 如图,AB是⊙O的弦,OD⊥OB,交AB于点E,且AD = ED. 求证:AD是⊙O的切线.

答案:
[证明]如图,连接OA.
∵OA=OB,
∴∠B=∠OAB.
∵AD=ED,
∴∠EAD=∠AED,
∵OD⊥OB,
∴∠BOD=90°.

∴∠B + ∠OEB = 90°.
∵∠OEB = ∠AED,
∴∠OEB = ∠EAD.
∴∠OAB + ∠EAD = 90°,
即∠OAD = 90°.
∴OA⊥AD.
∵OA是半径,
∴AD是⊙O的切线.
[证明]如图,连接OA.
∵OA=OB,
∴∠B=∠OAB.
∵AD=ED,
∴∠EAD=∠AED,
∵OD⊥OB,
∴∠BOD=90°.

∴∠B + ∠OEB = 90°.
∵∠OEB = ∠AED,
∴∠OEB = ∠EAD.
∴∠OAB + ∠EAD = 90°,
即∠OAD = 90°.
∴OA⊥AD.
∵OA是半径,
∴AD是⊙O的切线.
5. [2024江西]如图,AB是半圆O的直径,点D是弦AC延长线上一点,连接BD,BC,∠D = ∠ABC = 60°.
(1)求证:BD是半圆O的切线;
(2)当BC = 3时,求⌢AC的长.

(1)求证:BD是半圆O的切线;
(2)当BC = 3时,求⌢AC的长.

答案:
(1)[证明]
∵AB是半圆O的直径,
∴∠ACB = 90°.
∴∠A + ∠ABC = 90°.
∵∠D = ∠ABC,
∴∠D + ∠A = 90°.
∴∠ABD = 90°.
∴AB⊥BD.
∵AB是半圆O的直径,
∴BD是半圆O的切线.
(2)[解]连接OC,如图.
∵∠ABC = 60°,

∴∠AOC = 2∠ABC = 120°.
∵OC = OB,
∴△BOC是等边三角形.
∴OC = BC = 3.
∴$\overset{\frown}{AC}$的长为$\frac{120\pi\times3}{180}=2\pi$.
(1)[证明]
∵AB是半圆O的直径,
∴∠ACB = 90°.
∴∠A + ∠ABC = 90°.
∵∠D = ∠ABC,
∴∠D + ∠A = 90°.
∴∠ABD = 90°.
∴AB⊥BD.
∵AB是半圆O的直径,
∴BD是半圆O的切线.
(2)[解]连接OC,如图.
∵∠ABC = 60°,

∴∠AOC = 2∠ABC = 120°.
∵OC = OB,
∴△BOC是等边三角形.
∴OC = BC = 3.
∴$\overset{\frown}{AC}$的长为$\frac{120\pi\times3}{180}=2\pi$.
6. △ABC内接于⊙O,过点A作直线EF,已知∠B = ∠EAC,根据弦AB的变化,两人分别探究直线EF与⊙O的位置关系:
甲:如图①,当弦AB过点O时,EF与⊙O相切;乙:如图②,当弦AB不过点O时,EF与⊙O相切.
下列判断正确的是 ( )
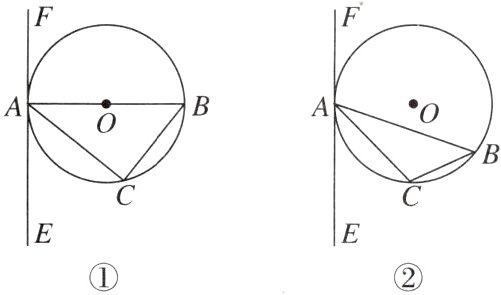
A. 甲对,乙不对
B. 甲不对,乙对
C. 甲和乙都对
D. 甲和乙都不对
甲:如图①,当弦AB过点O时,EF与⊙O相切;乙:如图②,当弦AB不过点O时,EF与⊙O相切.
下列判断正确的是 ( )

A. 甲对,乙不对
B. 甲不对,乙对
C. 甲和乙都对
D. 甲和乙都不对
答案:
C [点拨]对于甲:
∵AB过点O,
∴AB是⊙O的直径.
∴∠C = 90°.
∴∠B + ∠CAB = 90°.
∵∠EAC = ∠B,
∴∠EAC + ∠CAB = 90°.
∴EF⊥AB.
∵AB是⊙O的直径,
∴EF是⊙O的切线. 故甲对.
对于乙:如图,作直径AM,连接CM,则∠B = ∠M.
∵∠EAC = ∠B,
∴∠EAC = ∠M.
同甲可得EF⊥AM.
∵AM是⊙O的直径,
∴EF是⊙O的切线. 故乙对.

C [点拨]对于甲:
∵AB过点O,
∴AB是⊙O的直径.
∴∠C = 90°.
∴∠B + ∠CAB = 90°.
∵∠EAC = ∠B,
∴∠EAC + ∠CAB = 90°.
∴EF⊥AB.
∵AB是⊙O的直径,
∴EF是⊙O的切线. 故甲对.
对于乙:如图,作直径AM,连接CM,则∠B = ∠M.
∵∠EAC = ∠B,
∴∠EAC = ∠M.
同甲可得EF⊥AM.
∵AM是⊙O的直径,
∴EF是⊙O的切线. 故乙对.

7. [新视角 结论辨析题]题目:“如图,在等腰直角三角形ABC中,∠ABC = 90°,以点A为圆心,小于AB的长度为半径作⊙A,P是⊙A上一点,连接AP,BP. 将线段BP绕点B顺时针旋转90°得到线段BP',连接PP'. 当∠APB为多少度时,PP'与⊙A相切于点P?”对于其答案,甲答:∠APB = 135°,乙答:∠APB = 60°,丙答:∠APB = 45°,则下列选项中正确的是 ( )

A. 只有甲的答案对
B. 甲、丙的答案合在一起才完整
C. 乙、丙的答案合在一起才完整
D. 三人的答案合在一起才完整

A. 只有甲的答案对
B. 甲、丙的答案合在一起才完整
C. 乙、丙的答案合在一起才完整
D. 三人的答案合在一起才完整
答案:
B [点拨]①当点P在AB的左侧时,如图①,
由旋转的性质知BP = BP',∠PBP' = 90°,
∴∠BPP' = 45°.
当PP'是⊙A的切线时,AP⊥PP',
∴∠APP' = 90°.
∴∠APB = 90° + 45° = 135°;
②当点P在AB的右侧时,如图②,
同理可得∠BPP' = 45°,
当PP'是⊙A的切线时,AP⊥PP',

∴∠APP' = 90°.
∴∠APB = 90° - 45° = 45°.
∴甲、丙的答案合在一起才完整.
B [点拨]①当点P在AB的左侧时,如图①,
由旋转的性质知BP = BP',∠PBP' = 90°,
∴∠BPP' = 45°.
当PP'是⊙A的切线时,AP⊥PP',
∴∠APP' = 90°.
∴∠APB = 90° + 45° = 135°;
②当点P在AB的右侧时,如图②,
同理可得∠BPP' = 45°,
当PP'是⊙A的切线时,AP⊥PP',

∴∠APP' = 90°.
∴∠APB = 90° - 45° = 45°.
∴甲、丙的答案合在一起才完整.
查看更多完整答案,请扫码查看


