《2025年综合应用创新题典中点九年级数学下册冀教版》

1. 母题教材P45习题T1如图，某农场计划修建三间矩形饲养室，饲养室一面靠现有墙(墙可用长≤20 m)，中间用两道墙隔开，已知计划中的修筑材料可建围墙总长为60 m，设垂直于墙的一边长为x m，占地总面积为y m²，则y有 （ ）

A. 最小值200
B. 最小值225
C. 最大值200
D. 最大值225

答案： C

2. [2024唐山模拟] 某商店销售一批头盔，售价为每顶80元，每月可售出200顶. 在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶. 已知头盔的进价为每顶50元，则该商店每月销售头盔获得最大利润时，每顶头盔的售价为 （ ）
A. 50元
B. 90元
C. 80元
D. 70元

答案： D 【点拨】设每月获得利润为w元，每顶头盔的售价为x元，由题意可得w=(x - 50)[200 + (80 - x)×20]= - 20(x - 70)² + 8000，
∴当x = 70时，w取得最大值.

3. 如图，△ABC是直角三角形，∠A = 90°，AB = 8 cm，AC = 6 cm，点P从点A出发，沿AB方向以2 cm/s的速度向点B运动，同时点Q从点A出发，沿AC方向以1 cm/s的速度向点C运动，其中一个动点到达终点，则另一个动点也停止运动，则△APQ的最大面积是______.

答案： 16 cm² 【点拨】设点P的运动时间为t s，
∵点P从点A出发，沿AB方向以2 cm/s的速度向点B运动，同时点Q从点A出发，沿AC方向以1 cm/s的速度向点C运动，
∴AP = 2t cm，AQ = t cm.
∴S△APQ = t² cm². 易知0 ＜ t ≤ 4，
∴△APQ的最大面积是16 cm².
点方法 在解决有关利用二次函数求几何图形的最大（小）面积（或体积）的问题时，应遵循以下思路：
(1)利用几何图形的面积（或体积）公式得到关于面积（或体积）的二次函数的表达式；
(2)由已得到的二次函数的表达式求解问题；
(3)结合实际问题中自变量的取值范围得出实际问题的答案.

4. [2024滨州] 春节期间，全国各影院上映多部影片，某影院每天运营成本为2 000元，该影院每天售出的电影票数量y(单位：张)与售价x(30≤x≤80，且x是整数，单位：元/张)之间满足一次函数关系，部分数据如下表所示：

(1)请求出y与x之间的函数关系式.
(2)设该影院每天的利润(利润 = 票房收入 - 运营成本)为w(单位：元)，求w与x之间的函数关系式.
(3)该影院将电影票售价定为多少时，每天获利最大？最大利润是多少？

答案： 【解】
(1)设y与x之间的函数关系式是y = kx + b，
由表格，得{40k + b = 164，50k + b = 124}，
解得{k = - 4，b = 324}，
即y与x之间的函数关系式是y = - 4x + 324(30 ≤ x ≤ 80，且x是整数).
(2)由题意可得，
w = x( - 4x + 324) - 2000 = - 4x² + 324x - 2000，
即w与x之间的函数关系式是w = - 4x² + 324x - 2000(30 ≤ x ≤ 80，且x为整数).
(3)由
(2)知w = - 4x² + 324x - 2000 = - 4(x - $\frac{81}{2}$)² + 4561.
∵30 ≤ x ≤ 80，且x是整数，
∴当x = 40或41时，w取得最大值，最大值为4560.
答：该影院将电影票售价定为40元/张或41元/张时，每天获利最大，最大利润是4560元.

5. [2024张家口模拟] 九年级(1)班计划在劳动实践基地内种植蔬菜，班长买回来8 m长的围栏，准备围成一边靠墙(墙足够长)的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形，围成等腰三角形(底边靠墙)，围成半圆形这三种方案(如图)，则最佳方案是 （ ）

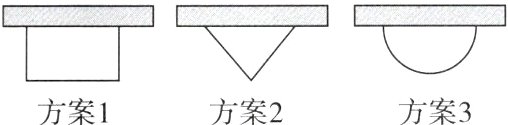
A. 方案1
B. 方案2
C. 方案3
D. 面积都一样

答案：
C 【点拨】方案1：如图①，设AD = x m，

则AB = (8 - 2x)m，则菜园面积为x(8 - 2x)= - 2x² + 8x = - 2(x - 2)² + 8，易知当x = 2时，菜园面积最大，最大面积为8 m²；
方案2：如图②，易知AB = AC = 4 m，过点B作BH⊥AC于点H，
则BH ≤ AB = 4 m.

∵S△ABC = $\frac{1}{2}$AC·BH，
∴当BH = 4 m时，菜园的面积最大，最大面积为$\frac{1}{2}$×4×4 = 8(m²)；
方案3：易知半圆形的半径为$\frac{8}{π}$m，
∴菜园的面积为$\frac{π×(\frac{8}{π})²}{2}$ = $\frac{32}{π}$(m²)＞8 m². 故选C.

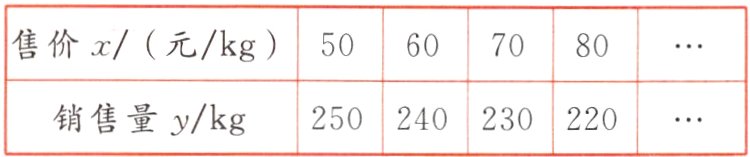
6. 某商店销售一种进价为40元/kg的海鲜产品，据调查发现，月销售量y(kg)与售价x(元/kg)之间满足一次函数关系，部分信息如下表，下列说法错误的是 （ ）

A. y与x之间的函数关系式为y = -x + 300
B. 当售价为72元时，月销售利润为7 296元
C. 当每月购进这种海鲜的总进价不超过5 000元时，最大利润可达到16 900元
D. 销售这种海鲜产品，每月最多可获得利润16 900元

答案： C 【点拨】设y与x之间的函数关系式为y = kx + b，
将(50，250)，(60，240)代入，得
{50k + b = 250，60k + b = 240}，解得{k = - 1，b = 300}.
∴y与x之间的函数关系式为y = - x + 300，故A正确.
当售价为72元时，月销售利润为(72 - 40)×( - 72 + 300)= 32×228 = 7296(元)，故B正确.
设月销售利润为W元，根据题意，得
W = (x - 40)y = (x - 40)( - x + 300)= - x² + 340x - 12000 = - (x - 170)² + 16900.
当每月购进这种海鲜的总进价不超过5000元时，
每月购进这种海鲜的质量最多为5000÷40 = 125(kg)，即y ≤ 125.
∴ - x + 300 ≤ 125，即x ≥ 175.
∴当x = 175时，W取得最大值，最大值为 - (175 - 170)² + 16900 = 16875，故C错误.
∵W = - (x - 170)² + 16900，
∴当x = 170时，W取最大值，最大值为16900，故D正确.