《2025年综合应用创新题典中点九年级数学下册冀教版》

1. 情境题 实物抽象 某市新建一座景观桥. 如图，桥的拱肋ADB可视为抛物线的一部分，桥面AB可视为水平线段，桥面与拱肋用垂直于桥面的杆状景观灯连接，拱肋的跨度AB为40 m，桥拱的最大高度CD为16 m，则与CD的距离为5 m的景观灯杆MN的高度为(不考虑灯杆和拱肋的粗细)
( )

A. 13 m
B. 14 m
C. 15 m
D. 16 m

答案：
C 【点拨】建立如图所示的平面直角坐标系，

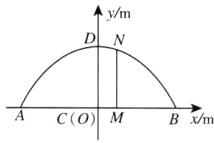
设抛物线的表达式为$y = ax^{2}+16$，
由题意可知，$B$的坐标为$(20,0)$，
$\therefore400a + 16 = 0$. $\therefore a=-\frac{1}{25}$.
$\therefore y = -\frac{1}{25}x^{2}+16$.
当$x = 5$时，$y = 15$.
$\therefore$与$CD$距离为$5m$的景观灯杆$MN$的高度为$15m$.
点技巧 解决抛物线形拱桥问题的一般思路：

2. [2024张家口模拟] 如图是一款抛物线形落地灯筒的示意图，防滑螺母C为抛物线形支架的最高点，灯罩D距离地面1.5 m，最高点C距灯柱AB的水平距离为1.6 m，灯柱AB = 1.5 m，若茶几摆放在灯罩的正下方，则茶几到灯柱的距离AE为
( )

A. 3.2 m
B. 0.32 m
C. 2.5 m
D. 1.6 m

答案： A 【点拨】$\because AB = DE = 1.5m$，
$\therefore$点$B$与点$D$关于抛物线的对称轴对称.
又$\because$点$C$为抛物线的顶点，且点$C$到灯柱$AB$的水平距离为$1.6m$，
$\therefore AE = 2\times1.6 = 3.2(m)$.

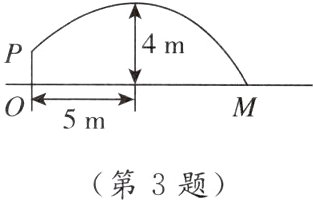
3. [2024广西] 如图，壮壮同学投掷实心球，出手(点P处)的高度OP是$\frac{7}{4}$ m，出手后实心球沿一段抛物线运行，到达最高点时，水平距离是5 m，高度是4 m. 若实心球落地点为M，则OM = ________m.

答案：
$\frac{35}{3}$ 【点拨】如图，以$O$为坐标原点，$OM$所在直线为$x$轴，$OP$所在直线为$y$轴，建立平面直角坐标系，

由题意可知，$P(0,\frac{7}{4})$，$B(5,4)$，其中$B$点为抛物线的顶点，
设抛物线的表达式为$y = a(x - 5)^{2}+4$，
将$P(0,\frac{7}{4})$代入，得$25a + 4=\frac{7}{4}$，解得$a = -\frac{9}{100}$，
$\therefore$抛物线的表达式为$y = -\frac{9}{100}(x - 5)^{2}+4$，
令$-\frac{9}{100}(x - 5)^{2}+4 = 0$，解得$x_{1}=\frac{35}{3}$，$x_{2}=-\frac{5}{3}$（舍去），
$\therefore OM=\frac{35}{3}m$.

4. 如图，杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端B处的椅子上，其身体(看成一点)的运动路线是抛物线$y = -\frac{3}{5}x^{2}+3x + 1$的一部分.
(1)求演员弹跳时离地面的最大高度.
(2)已知人梯高BC = 3.4 m，在一次表演中，人梯到起跳点A的水平距离是4 m，问这次表演能否成功？请说明理由.

答案： 【解】
(1)$\because y = -\frac{3}{5}x^{2}+3x + 1 = -\frac{3}{5}(x-\frac{5}{2})^{2}+\frac{19}{4}$，
$\therefore$当$x=\frac{5}{2}$时，$y$有最大值，$y_{最大值}=\frac{19}{4}=4.75$.
$\therefore$演员弹跳时离地面的最大高度是$4.75m$.
(2)能成功. 理由：由题意知$B(4,3.4)$.
对于$y = -\frac{3}{5}x^{2}+3x + 1$，当$x = 4$时，$y = -\frac{3}{5}\times4^{2}+3\times4 + 1 = 3.4$.
即点$B(4,3.4)$在抛物线$y = -\frac{3}{5}x^{2}+3x + 1$上，
$\therefore$能表演成功.

5. 新考向 传统文化 刀削面堪称天下一绝，传统的操作方法是一手托面，一手拿刀，直接将面削到开水锅里. 如图，面刚被削离时与开水锅的高度差h = 0.45 m，与锅的水平距离L = 0.3 m，锅的半径R = 0.5 m. 若将削出的小面圈的运动轨迹视为抛物线的一部分，要使其落入锅中(锅的厚度忽略不计)，则其水平初速度$v_{0}$不可能为(提示：$h=\frac{1}{2}gt^{2}$，$g = 10 m/s^{2}$，水平移动距离$s = vt$)
( )

A. 2.5 m/s
B. 3 m/s
C. 3.5 m/s
D. 5 m/s

答案： D 【点拨】$\because h=\frac{1}{2}gt^{2}$，$\therefore t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times0.45}{10}} = 0.3(s)$.
$\because L\lt v_{0}t\lt L + 2R$，
$\therefore$最小水平初速度为$\frac{L}{t}=\frac{0.3}{0.3}=1(m/s)$，
最大水平初速度为$\frac{L + 2R}{t}=\frac{0.3+2\times0.5}{0.3}=\frac{13}{3}(m/s)$.
由此可知，选项A，B，C都在此范围内，不符合题意，选项D不在此范围内，符合题意.