《2025年学习检测九年级数学下册华师大版》

3. 若正多边形的中心角为40°，则这个正多边形的边数为【 】
A. 8
B. 9
C. 10
D. 11

答案： B.

4. 正六边形的边长与它的半径之间的大小关系是【 】
A. 边长大于半径
B. 相等
C. 边长小于半径
D. 不能确定

答案： B.

5. 下列图形中不一定有外接圆的是【 】
A. 三角形
B. 矩形
C. 菱形
D. 正方形

答案： C.

6. 把正五边形绕着它的中心旋转，下面给出的四个旋转角度中，得到的正五边形能与原来的正五边形重合的是【 】
A. 144°
B. 180°
C. 240°
D. 366°

答案： A.

7. 若一个正多边形的每一个内角都等于120°，则它的中心角等于【 】
A. 120°
B. 90°
C. 60°
D. 30°

答案： C.

8. 半径相等的圆内接正三角形、正方形、正六边形的边长之比为【 】
A. 1∶$\sqrt{2}$∶$\sqrt{3}$
B. $\sqrt{3}$∶$\sqrt{2}$∶1
C. 1∶2∶3
D. 3∶2∶1

答案： B.

9. 如图，在半径为R的圆内作一个内接正方形，然后作这个正方形的内切圆，再在这个内切圆中作内接正方形，依此作第n个内切圆，它的半径是【 】

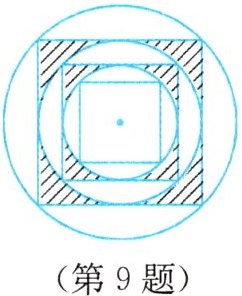
A. $(\frac{\sqrt{2}}{2})^nR$
B. $(\frac{1}{2})^nR$
C. $(\frac{1}{2})^{n - 1}R$
D. $(\frac{\sqrt{2}}{2})^{n - 1}R$

答案： A.

10. 用一个圆形纸片剪成一个边长为6 cm的正六边形，则圆形纸片的半径最小为______cm.

答案： 6.

11. 若正六边形外接圆的半径是2，则正六边形的面积是______.

答案： $6\sqrt{3}$.

12. 若⊙O的半径R = 5，则其内接正方形的边心距为______.

答案： $\frac{5\sqrt{2}}{2}$.

13. 若⊙O的直径d = 8，则其内接正三角形的边长为______.

答案： $4\sqrt{3}$.

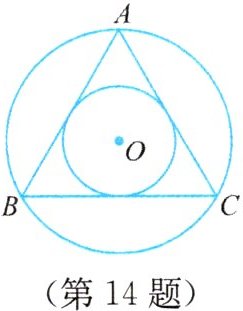
14. 如图，正三角形ABC的边长为2，求其内切圆的半径r和外接圆的半径R.

答案： $r = \frac{\sqrt{3}}{3}, R = \frac{2\sqrt{3}}{3}$. 提示：连接 $OC$，过 $O$ 作 $OD\perp BC$ 于 $D$.