《2025年学习检测九年级数学下册华师大版》

15. 当$k$取何值时，$y=(k - 2)x^{k^{2}+k - 2}$是二次函数?

答案： $k=\frac{-1\pm\sqrt{17}}{2}$.

16. 如图，某校小农场要盖一排三间长方形的羊圈，打算一面利用一堵旧墙，其余各面用木材围成栅栏，该校计划用木材围出总长24 m的栅栏. 设每间羊圈的长为$x$ m.
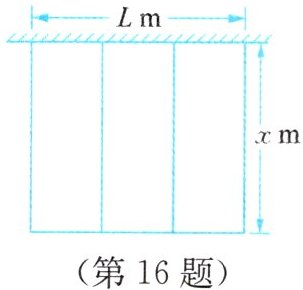
(1) 用含$x$的代数式分别表示围成的三间羊圈所利用的旧墙的总长度$L$(m)和三间羊圈的总面积$S$(m²).
(2) $S$可以看成$x$的什么函数? 这里的自变量$x$的取值有什么限制?
(3) 请计算，当$x$分别为2、3、4、5时，羊圈的总面积分别为多少平方米? 在这些数值中，$x$取哪个时，总面积最大?

答案：
(1) $L = 24 - 4x$, $S = -4x^{2}+24x$;
(2) $S$可以看成 $x$的二次函数, $0 ＜ x ＜ 6$;
(3) 对应的总面积分别为 $32m^{2}$、$36m^{2}$、$32m^{2}$、$20m^{2}$. 当 $x = 3$时, 总面积最大.