《2025年学习检测九年级数学下册华师大版》

4. 苹果熟了，从树上落下所经过的路程$s$与下落的时间$t$满足$s=\frac{1}{2}gt^{2}$（$g$是不为0的常数），则$s$与$t$的函数图象大致是【 】

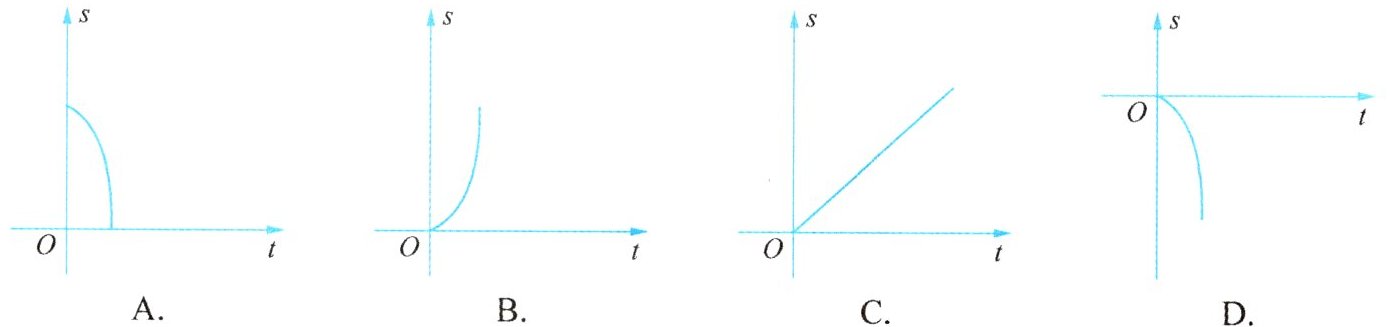
答案： B.

5. 抛物线$y = 4x^{2}-x - 3$与$y$轴的交点坐标是________，与$x$轴的交点坐标是________.

答案： $(0,-3);(1,0),(-\frac{3}{4},0)$.

6. 若抛物线$y = x^{2}+bx + c$与$x$轴交于点$(-2,0)$，$(5,0)$，则$b =$_______，$c =$_______.

答案： $-3,-10$.

7. 某抛物线$y = ax^{2}+bx + c$的形状如图所示，则一元二次方程$ax^{2}+bx + c = 0$的解为_______；不等式$ax^{2}+bx + c ＞ 0$的解集为_______；不等式$ax^{2}+bx + c ＜ 0$的解集为_______.

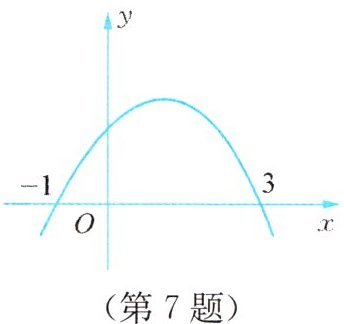
答案： $x_1 = -1,x_2 = 3$; $-1 ＜ x ＜ 3$; $x ＜ -1$或$x ＞ 3$.

8. 如图，一桥拱呈抛物线形状，桥的最大高度是16米，跨度是40米，在线段$AB$上离中心$D$点5米的$M$处，桥的高度是_______米.

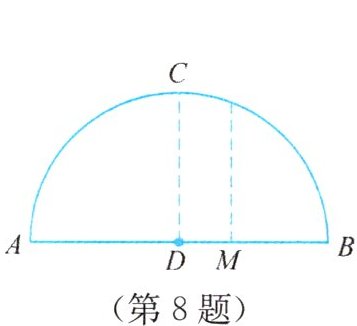
答案： 15.

9. 某涵洞的截面是抛物线形，如图所示，在图中建立的直角坐标系中，抛物线的解析式为$y =-\frac{1}{4}x^{2}$，当涵洞水面宽$AB$为12米时，水面到桥拱顶点$O$的距离为_______米.

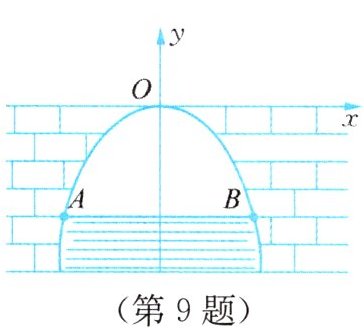
答案： 9.

10. 某产品每件的成本为10元，在试销阶段每件产品的日销售价$x$（元）与产品的日销售量$y$（件）之间的关系如下表：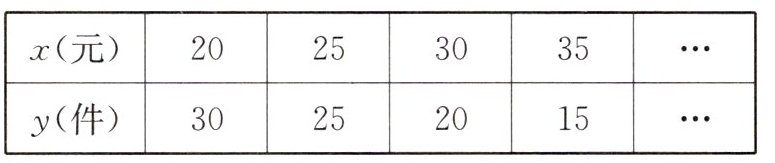
(1) 在草稿纸上描点，观察点的分布，确定$y$与$x$之间的函数关系式；
(2) 要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？

答案：
(1) $y = -x + 50$;
(2) 当每件产品的销售价定为30元时,每日销售利润最大是400元.