《2025年学习检测九年级数学下册华师大版》

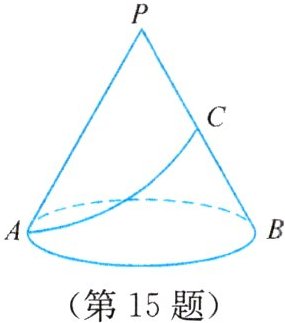
15.有一个圆锥体形状的粮仓,如图所示，一只猫在A处发现PB中点C处有一只老鼠在偷吃粮食,已知圆锥底面积为25πcm²,母线长为10cm,若猫在粮仓面上捉老鼠,则猫由A点到C点的最短路程是多少？
　　　　　

答案： 设底面半径为 $r$，因为 $\pi r^{2}=25\pi$，所以 $r = 5$，所以 $C_{周长}=2\pi r=\frac{n\pi R}{180}$，$2\pi\times5=\frac{n\pi\times10}{180}$，所以 $n = 180^{\circ}$. 把圆锥侧面展开可知，$\angle APC = 90^{\circ}$，所以 $A$ 点到 $C$ 点的最短路程为 $\sqrt{10^{2}+5^{2}} = 5\sqrt{5}(\mathrm{cm})$.

1. 圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的大小是【 】
A. 36°
B. 60°
C. 72°
D. 108°

答案： C.

2. 下列说法中，不正确的是【 】
A. 各边相等、各角也相等的多边形是正多边形
B. 各边相等的圆内接多边形是正多边形
C. 各角相等的圆内接多边形是正多边形
D. 正多边形一定是轴对称图形，但不一定是中心对称图形

答案： C.