《2025年学习检测九年级数学下册华师大版》

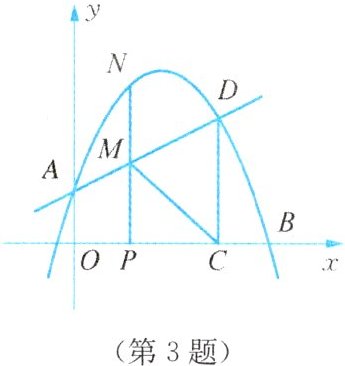
3. 【菏泽中考】如图，抛物线$y = ax^{2}+bx + 1$交$y$轴于点$A$，交$x$轴于点$B(4,0)$，与过点$A$的直线相交于另一点$D(3,\frac{5}{2})$，过点$D$作$DC\perp x$轴，垂足为点$C$. 点$P$在$x$轴正半轴上，过点$P$作$PN\perp x$轴，交直线$AD$于点$M$，交抛物线于点$N$，设$OP$的长为$t$.
(1) 求抛物线的函数表达式；
(2) 若点$P$在线段$OC$上(不与点$O$、$C$重合)，求$\triangle PCM$面积的最大值；
(3) 是否存在$t$，使以点$M$，$C$，$D$，$N$为顶点的四边形是平行四边形？请说明理由.

答案：
(1) 把点$B$和点$D$的坐标分别代入$y = ax^{2}+bx + 1$中，求得抛物线的表达式为$y=-\frac{3}{4}x^{2}+\frac{11}{4}x + 1$.
(2) 设直线$AD$为$y = kx + b$，把点$A$和点$D$的坐标分别代入，求得$y=\frac{1}{2}x + 1$. 设$P(t,0)$，则$M(t,\frac{1}{2}t + 1)$，$PM=\frac{1}{2}t + 1$. 因为$CD\perp x$轴，所以$PC = 3 - t$. 所以$S_{\triangle PCM}=\frac{1}{2}PC\cdot PM=\frac{1}{2}(3 - t)(\frac{1}{2}t + 1)=-\frac{1}{4}(t-\frac{1}{2})^{2}+\frac{25}{16}$. 所以$\triangle PCM$面积的最大值是$\frac{25}{16}$.
(3) $M(t,\frac{1}{2}t + 1)$，$N(t,\frac{3}{4}t^{2}+\frac{11}{4}t + 1)$，所以$MN=\vert PM - PN\vert=\vert\frac{3}{4}t^{2}-\frac{9}{4}t\vert$. 若以点$M$、$C$、$D$、$N$为顶点的四边形是平行四边形，则$MN = CD$，即$-\frac{3}{4}t^{2}+\frac{9}{4}t=\frac{5}{2}$或$\frac{3}{4}t^{2}-\frac{9}{4}t=\frac{5}{2}$. 解这两个方程，一个方程无解，另一个方程的解为$t_{1}=\frac{9+\sqrt{201}}{6}$，$t_{2}=\frac{9-\sqrt{201}}{6}$（舍去）. 所以符合条件的平行四边形有1个.

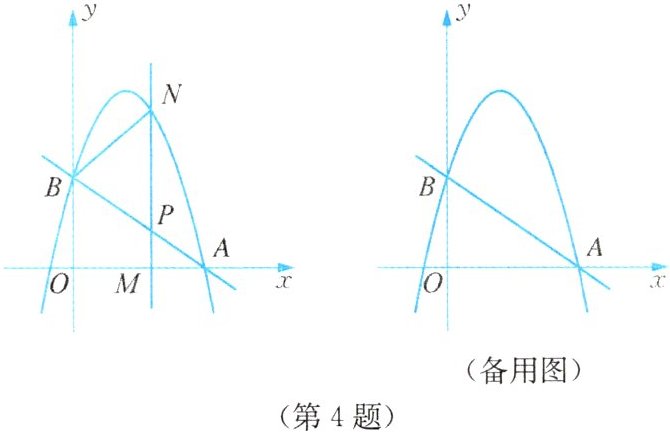
4. 【河南中考】如图，直线$y = -\frac{2}{3}x + c$与$x$轴交于点$A(3,0)$，与$y$轴交于点$B$，抛物线$y = -\frac{4}{3}x^{2}+bx + c$经过点$A$，$B$.
(1) 求点$B$的坐标和抛物线的解析式.
(2) $M(m,0)$为$x$轴上一动点，过点$M$且垂直于$x$轴的直线与直线$AB$及抛物线分别交于点$P$，$N$.
① 点$M$在线段$OA$上运动，若以$B$，$P$，$N$为顶点的三角形与$\triangle APM$相似，求点$M$的坐标.
② 点$M$在$x$轴上自由运动，若三个点$M$，$P$，$N$中恰有一点是其他两点所连线段的中点(三点重合除外)，则称$M$，$P$，$N$三点为“共谐点”. 请直接写出使得$M$，$P$，$N$三点成为“共谐点”的$m$的值.

答案：

(1) 因为直线与$x$轴交于点$A(3,0)$，所以$-\frac{2}{3}\times3 + c = 0$，解得$c = 2$，即$B(0,2)$. 因为抛物线过点$A(3,0)$，所以$-\frac{4}{3}\times3^{2}+3b + 2 = 0$，解得$b=\frac{10}{3}$. 所以抛物线的函数表达式为$y=-\frac{4}{3}x^{2}+\frac{10}{3}x + 2$.
(2) 因为$MN\perp x$轴，$M(m,0)$，所以$N(m,-\frac{4}{3}m^{2}+\frac{10}{3}m + 2)$. ①由点$A(3,0)$，$B(0,2)$，得$OA = 3$，$OB = 2$. 由$\angle APM=\angle BPN ＜ 90^{\circ}$，$\angle AMP = 90^{\circ}$可得，若使$\triangle BPN$与$\triangle APM$相似，需使$\angle NBP = 90^{\circ}$或$\angle BNP = 90^{\circ}$. 当$\angle BNP = 90^{\circ}$时，过点$N$作$NC\perp y$轴于点$C$. 于是可得$\angle NBC+\angle BNC = 90^{\circ}$，$NC = m$，$BC=-\frac{4}{3}m^{2}+\frac{10}{3}m$. 由$\angle NBP = 90^{\circ}$知$\angle NBC+\angle ABO = 90^{\circ}$. 所以$\angle ABO=\angle BNC$. 所以$Rt\triangle BNC\sim Rt\triangle ABO\sim Rt\triangle APM$. 所以$\frac{NC}{OB}=\frac{CB}{OA}$，即$\frac{m}{2}=\frac{-\frac{4}{3}m^{2}+\frac{10}{3}m}{3}$，解得$m_{1}=\frac{11}{8}$，$m_{2}=0$（舍去），即$M(\frac{11}{8},0)$. 当$\angle BNP = 90^{\circ}$时，$BN\perp NM$，所以$-\frac{4}{3}m^{2}+\frac{10}{3}m + 2 = 2$，解得$m_{3}=\frac{5}{2}$，$m_{4}=0$（舍去），即$M(\frac{5}{2},0)$. 综上，点$M$的坐标为$(\frac{11}{8},0)$或$(\frac{5}{2},0)$. ②$m=-1$，或$m = -\frac{1}{4}$，或$m=\frac{1}{2}$.