《2025年顶尖课课练七年级数学下册人教版》

12. 计算：
（1）$\sqrt{169\times196}$；
（2）$\sqrt{3}(2\sqrt{3}-3)$；
（3）$\vert 1-\sqrt{2}\vert-\vert \sqrt{3}-\sqrt{2}\vert-\vert \sqrt{3}-2\vert$；
（4）$\sqrt{6}-\sqrt{6}\left(\sqrt{6}+\frac{1}{\sqrt{6}}\right)$；
（5）$\vert \sqrt{2}-1\vert+\sqrt{2^{2}}+\sqrt[3]{-8}$；
（6）$\sqrt{2}\left(3\sqrt{2}+\frac{3}{\sqrt{2}}\right)-\sqrt{(-2)^{2}}+\sqrt[3]{(-1)^{3}}$.

答案： 182@@$6 - 3\sqrt{3}$@@$2\sqrt{2}-3$@@$\sqrt{6}-7$@@$\sqrt{2}-1$@@6

13. 如图 8.3.2 - 3，数轴上的点 $A$，$B$ 分别表示实数 $a$，$b$，则$\frac{1}{a}$ _______$\frac{1}{b}$.（填 “$＞$”、“$=$” 或 “$＜$”）

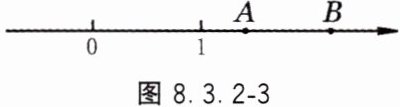
答案： ＞

14. 满足$\sqrt{11}\geqslant k$ 的最大整数 $k$ 是 ____.

答案： 3

15. 已知点 $A$ 在数轴上和原点相距 $3$ 个单位长度，点 $B$ 在数轴上和原点相距 $\sqrt{5}$ 个单位长度，则 $A$，$B$ 两点之间的距离是 ________________.

答案： $3 + \sqrt{5}$ 或 $3 - \sqrt{5}$

16. 如果 $a$ 是$\sqrt{15}$ 的整数部分，$b$ 是$\sqrt{15}$ 的小数部分，那么 $a - b =$ ________.

答案： $6-\sqrt{15}$

17. 将非负实数 $x$ “四舍五入” 到个位的值记为 $[x]$，当 $n$ 为非负整数时：
① 若 $n-\frac{1}{2}\leqslant x ＜ n+\frac{1}{2}$，则 $[x]=n$；
② 若 $[x]=n$，则 $n-\frac{1}{2}\leqslant x ＜ n+\frac{1}{2}$.
如 $[0]=[0.49]=0$，$[0.64]=[1.49]=1$，$[2]=2$.
（1）$[\pi]=$ ____；
（2）若 $\vert t + 1\vert=\frac{3}{2}t$，求满足条件的实数 $t$ 的值.

答案： 3@@$t = 2$