第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
10. 如图 7.3.1 - 3,已知 AE⊥BC,FG⊥BC,∠1 = ∠2,∠D = ∠3 + 50°,∠CBD = 80°.
(1)求证:AB//CD;
(2)求∠C 的度数.

(1)求证:AB//CD;
(2)求∠C 的度数.

答案:
略@@25°
11.(数学活动)如图 7.3.1 - 4①,在数学课上,同学们探究过直线 AB 外一点 P 画 CD//AB 的方法,其中小玲是通过折纸的方式完成的:
第一步:如图 7.3.1 - 4②,过点 P 进行第一次折叠,使点 B 的对称点 B′落在 AB 上,折痕 PQ 与 AB 相交于点 Q,打开纸张铺平;
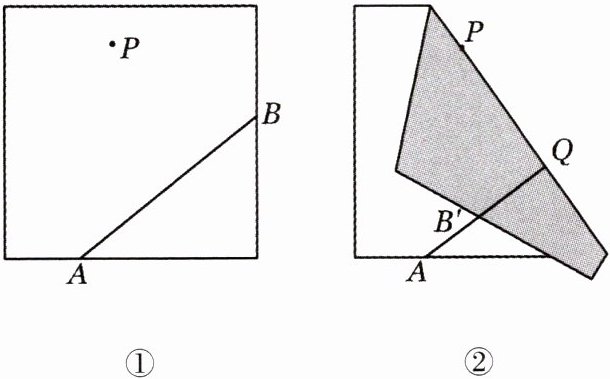
第二步:如图 7.3.1 - 4③,过点 P 进行第二次折叠,使折痕 CD⊥PQ,打开纸张铺平(如图 7.3.1 - 4④).
小玲就说 CD//AB,你能用几何推理说说其中的道理吗?
请完成下面的证明,并填上对应的推理根据.
证明:∵∠AQB = 180°,
∴∠__________ = $\frac{1}{2}$∠AQB = ______°.
理由是:(角平分线的定义).
∵CD⊥PQ,
∴∠__________ = 90°.
理由是:(______________).
∴ ______________.
∴CD//AB.
理由是:(______________).
第一步:如图 7.3.1 - 4②,过点 P 进行第一次折叠,使点 B 的对称点 B′落在 AB 上,折痕 PQ 与 AB 相交于点 Q,打开纸张铺平;


第二步:如图 7.3.1 - 4③,过点 P 进行第二次折叠,使折痕 CD⊥PQ,打开纸张铺平(如图 7.3.1 - 4④).
小玲就说 CD//AB,你能用几何推理说说其中的道理吗?
请完成下面的证明,并填上对应的推理根据.
证明:∵∠AQB = 180°,
∴∠__________ = $\frac{1}{2}$∠AQB = ______°.
理由是:(角平分线的定义).
∵CD⊥PQ,
∴∠__________ = 90°.
理由是:(______________).
∴ ______________.
∴CD//AB.
理由是:(______________).
答案:
AQP@@90@@CPQ@@∠AQP + ∠CPQ = 180°(理由略)
12. 如图 7.3.1 - 5,∠1 = ∠BCE,∠2 + ∠3 = 180°.
(1)判断 AC 与 EF 的位置关系,并说明理由;
(2)若 CA 平分∠BCE,EF⊥BF 于点 F,∠1 = 70°,求∠BAD 的度数.

(1)判断 AC 与 EF 的位置关系,并说明理由;
(2)若 CA 平分∠BCE,EF⊥BF 于点 F,∠1 = 70°,求∠BAD 的度数.

答案:
AC // EF,理由略@@55°
查看更多完整答案,请扫码查看


