《2025年小题狂做高中数学选择性必修第三册人教版》

1. 若变量$x$，$Y$之间是线性相关关系，则由以下数据表得到的经验回归直线必过定点



A.(2,6)
B.(3,8)
C.(4,9)
D.(5,10)

答案： 1. B 由表格中的数据可得$\bar{x}=\frac{1 + 2 + 4 + 5}{4}=3$，$\bar{y}=\frac{7 + 6 + 9 + 10}{4}=8$，则样本点的中心的坐标为$(3,8)$，即经验回归直线必过定点$(3,8)$。

2. 下列说法正确的是()

A.残差图中残差点所在的水平带状区域越宽，则经验回归方程的预测精确度越高
B.样本相关系数$r$越大，成对样本数据的线性相关性越强；反之，线性相关性越弱
C.经验回归直线就是散点图中经过样本数据点最多的那条直线
D.若甲、乙两个模型的决定系数$R^2$分别约为 0.88 和 0.80，则模型甲的拟合效果更好

答案： 2. D 对于A，残差图中残差点所在的水平带状区域越窄，则经验回归方程的预测精确度越高，A错误.对于B，样本相关系数$r$的绝对值越大，成对样本数据的线性相关性越强；反之，线性相关性越弱，B错误.对于C，经验回归直线就是散点图中，从整体上看大致在一条直线附近的那条直线，并不一定是经过数据点最多的直线，C错误.对于D，决定系数$R^2$越大，则拟合效果越好，由于$0.88＞0.80$，所以模型甲的拟合效果更好，D正确.

3. 某校一个课外学习小组为研究某作物种子的发芽率$Y$和温度$x$（单位：$^{\circ}C$）的关系，在 20 个不同的温度条件下进行种子发芽实验，由实验数据$(x_i,y_i)(i = 1,2,·s,20)$得到下面的散点图：

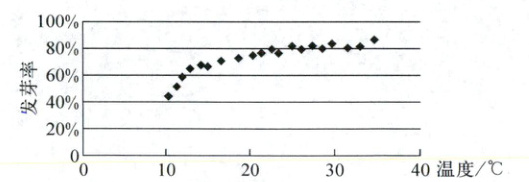
由此散点图判断，在 10$^{\circ}C$至 40$^{\circ}C$之间，下面四个经验回归方程类型中最适宜作为发芽率$Y$和温度$x$的经验回归方程模型的是

A.$y = a + bx$
B.$y = a + bx^2$
C.$y = a + be^x$
D.$y = a + b\ln x$

答案： 3. D 由散点图得种子的发芽率随温度的增高，先增大较快，后增大较慢，符合对数函数图象的特点，故D正确.

4. 易错易混 对于数据组$(x_i,y_i)(i = 1,2,·s,n)$，如果由经验回归方程得到的对应自变量$x_i$的预测值是$\hat{y}_i$，那么将$y_i - \hat{y}_i$称为样本点$(x_i,y_i)$处的残差. 某商场为了给一种新商品进行合理定价，将该商品按事先拟定的价格进行试销，得到下表所示数据. 若某商品销量$Y$(单位：件)与单价$x$(单位：元)之间的经验回归方程为$\hat{y} = -20x + a$，且样本点$(8.4,82)$处的残差为 2，则$m =$


A.66
B.68
C.70
D.72

答案： 4. B 由条件知当$x_2 = 8.4$时，$\hat{y}_2 = 82 - 2 = 80$，代入$\hat{y} = -20x + a$，解得$a = 80 + 20×8.4 = 248$，于是$\hat{y} = -20x + 248$.又$\bar{x}=\frac{8.2 + 8.4 + 8.6 + 8.8}{4}=8.5$，所以$\hat{y} = -20×8.5 + 248 = 78$，即$\frac{84 + 82 + 78 + m}{4}=78$，解得$m = 68$.
易错警示 样本点不一定在经验回归直线上，故本题不能将$x = 8.8$代入方程求$m$.

5. 教材变式 某戏曲相关部门对陕西关中地区进行了“喜爱看秦腔”的调查，发现年龄段与爱看秦腔的人数比存在较好的线性相关关系，年龄在$[40,44]$，$[45,49]$，$[50,54]$，$[55,59]$的爱看人数比分别是 0.10,0.18,0.20,0.30，现用各年龄段的中间值代表年龄段，如 42 代表$[40,44]$. 由此求得爱看人数比$Y$关于年龄段$x$的经验回归方程为$\hat{y} =$
$kx - 0.4188$. 则年龄在$[60,64]$的 10 000 人中，爱看秦腔的人数约为

A.4 200
B.3 900
C.3 700
D.3 500

答案： 5. D 由题意各年龄段的中间值为42，47，52，57，则$\bar{x}=\frac{42 + 47 + 52 + 57}{4}=49.5$.又$\bar{y}=\frac{0.10 + 0.18 + 0.20 + 0.30}{4}=0.195$，代入$y = kx - 0.4188$，解得$k = 0.0124$.取$x = 62$，得$y = 0.0124×62 - 0.4188 = 0.35$，所以年龄在$[60,64]$内的10000人中的人数为$0.35×10000 = 3500$.
教材链接（选择性必修三习题8.2.2练习1第2题改编）