2025年小题狂做高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 设随机变量 $ X \sim B \left( 6 , \frac { 1 } { 2 } \right) $,则 $ P ( X = 3 ) = $
(
A.$ \frac { 5 } { 1 6 } $
B.$ \frac { 3 } { 1 6 } $
C.$ \frac { 5 } { 8 } $
D.$ \frac { 7 } { 1 6 } $
(
A
)A.$ \frac { 5 } { 1 6 } $
B.$ \frac { 3 } { 1 6 } $
C.$ \frac { 5 } { 8 } $
D.$ \frac { 7 } { 1 6 } $
答案:
1. A 由二项分布的概率公式可得,$P(X=3)=C_{3}^{3}×(\frac{1}{2})^{3}×(\frac{1}{2})^{3}=\frac{5}{16}$;
2. 根据历史数据统计,长江中下游某地区在黄梅时节,每天下雨的概率均为 $ \frac { 4 } { 5 } $. 假设每天是否下雨互不影响,则该地区黄梅时节连续两天中至少有一天下雨的概率为
(
A.$ \frac { 2 4 } { 2 5 } $
B.$ \frac { 1 6 } { 2 5 } $
C.$ \frac { 8 } { 2 5 } $
D.$ \frac { 4 } { 2 5 } $
(
A
)A.$ \frac { 2 4 } { 2 5 } $
B.$ \frac { 1 6 } { 2 5 } $
C.$ \frac { 8 } { 2 5 } $
D.$ \frac { 4 } { 2 5 } $
答案:
2. A 依题意,该地区黄梅时节连续两天中至少有一天下雨的概率为$p=C_{2}^{1}×\frac{4}{5}×(1-\frac{4}{5})+C_{2}^{2}×(\frac{4}{5})^{2}=\frac{24}{25}$.
3. 在 4 重伯努利试验中,若事件 A 至少发生 1 次的概率为 $ \frac { 6 5 } { 8 1 } $,则事件 A 在单次试验中发生的概率为
(
A.$ \frac { 1 } { 3 } $
B.$ \frac { 2 } { 5 } $
C.$ \frac { 5 } { 6 } $
D.$ \frac { 3 } { 4 } $
(
A
)A.$ \frac { 1 } { 3 } $
B.$ \frac { 2 } { 5 } $
C.$ \frac { 5 } { 6 } $
D.$ \frac { 3 } { 4 } $
答案:
3. A 设事件$A$在每次试验中发生的概率为$p$,由题意得$1-C_{4}^{0}p^{0}(1-p)^{4}=\frac{65}{81}$,所以$1-p=\frac{2}{3}$,即$p=\frac{1}{3}$.
4. 一袋中有 5 个白球、3 个红球,现从袋中往外取球,每次 1 个,记下颜色后放回,直到红球出现 10 次时停止,设停止时共取了 $ X $ 次球,则 $ P ( X = 1 2 ) = $
(
A.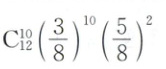
B.
C.
D.
(
D
)A.
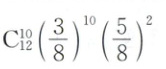
B.

C.

D.

答案:
4. D 由题意可得,取得红球的概率为$\frac{3}{8}$,$P(X=12)$说明前11次取球中,有9次取得红球、2次取得白球,且第12次取得红球,故$P(X=12)=C_{11}^{9}×(\frac{3}{8})^{9}×(\frac{5}{8})^{2}×\frac{3}{8}=C_{11}^{9}×(\frac{3}{8})^{10}×(\frac{5}{8})^{2}$.
5. 某学生参加一次选拔考试,有 5 道题,每题 10 分. 已知他解题的正确率为 $ \frac { 3 } { 5 } $,若 40 分为被选中的最低分数线,则该生被选中的概率是
(
A.$ C$${ 5 } ^ { 4 } × \left( \frac { 3 } { 5 } \right) ^ { 4 } × \frac { 2 } { 5 } $
B.$ C$${ 5 } ^ { 5 } \left( \frac { 3 } { 5 } \right) ^ { 5 } $
C.$ C$${ 5 } ^ { 4 } × \left( \frac { 3 } { 5 } \right) ^ { 4 } × \frac { 2 } { 5 } + C$${ 5 } ^ { 5 } \left( \frac { 3 } { 5 } \right) ^ { 5 } $
D.$ 1 - C$${ 5 } ^ { 3 } × \left( \frac { 3 } { 5 } \right) ^ { 3 } × \left( \frac { 2 } { 5 } \right) ^ { 2 } $
(
C
)A.$ C$${ 5 } ^ { 4 } × \left( \frac { 3 } { 5 } \right) ^ { 4 } × \frac { 2 } { 5 } $
B.$ C$${ 5 } ^ { 5 } \left( \frac { 3 } { 5 } \right) ^ { 5 } $
C.$ C$${ 5 } ^ { 4 } × \left( \frac { 3 } { 5 } \right) ^ { 4 } × \frac { 2 } { 5 } + C$${ 5 } ^ { 5 } \left( \frac { 3 } { 5 } \right) ^ { 5 } $
D.$ 1 - C$${ 5 } ^ { 3 } × \left( \frac { 3 } { 5 } \right) ^ { 3 } × \left( \frac { 2 } { 5 } \right) ^ { 2 } $
答案:
5. C 依题意可知,学生必须答对4道题或者5道题才能够被选上,答对4道题的概率为$C_{4}^{3}·(\frac{3}{5})^{3}×\frac{2}{5}$,答对5道题的概率为$C_{5}^{3}×(\frac{3}{5})^{3}$,故该生被选中的概率是$C_{4}^{3}×(\frac{3}{5})^{3}×\frac{2}{5}+C_{5}^{3}×(\frac{3}{5})^{3}$.
6. 若随机变量 $ X $ 服从二项分布 $ X \sim B ( 6 , p ) $,且 $ P ( X = 3 ) = \frac { 5 } { 1 6 } $,则 $ E ( X ^ { 2 } ) = $
(
A.$ \frac { 1 9 } { 2 } $
B.10
C.$ \frac { 2 1 } { 2 } $
D.11
(
C
)A.$ \frac { 1 9 } { 2 } $
B.10
C.$ \frac { 2 1 } { 2 } $
D.11
答案:
6. C 因为$X\sim B(6,p)$,所以$P(X=3)=C_{6}^{3}p^{3}·(1-p)^{3}=\frac{5}{16}$,所以$p^{3}(1-p)^{3}=\frac{1}{64}$,解得$p=\frac{1}{2}$,所以$P(X=0)=C_{6}^{0}×(\frac{1}{2})^{6}=\frac{1}{64}$,$P(X=1)=C_{6}^{1}×(\frac{1}{2})^{6}=\frac{3}{32}$,$P(X=2)=C_{6}^{2}×(\frac{1}{2})^{6}=\frac{15}{64}$,$P(X=3)=C_{6}^{3}×(\frac{1}{2})^{6}=\frac{5}{16}$,$P(X=4)=C_{6}^{4}×(\frac{1}{2})^{6}=\frac{15}{64}$,$P(X=5)=C_{6}^{5}×(\frac{1}{2})^{6}=\frac{3}{32}$,$P(X=6)=C_{6}^{6}×(\frac{1}{2})^{6}=\frac{1}{64}$,所以$X$的分布列为
$X$ 0 1 2 3 4 5 6
$P$ $\frac{1}{64}$ $\frac{3}{32}$ $\frac{15}{64}$ $\frac{5}{16}$ $\frac{15}{64}$ $\frac{3}{32}$ $\frac{1}{64}$
所以$X^{2}$的分布列为
$X^{2}$ 0 1 4 9 16 25 36
$P$ $\frac{1}{64}$ $\frac{3}{32}$ $\frac{15}{64}$ $\frac{5}{16}$ $\frac{15}{64}$ $\frac{3}{32}$ $\frac{1}{64}$
所以$E(X^{2})=1×\frac{3}{32}+4×\frac{15}{64}+9×\frac{5}{16}+16×\frac{15}{64}+25×\frac{3}{32}+36×\frac{1}{64}=\frac{21}{2}$.
$X$ 0 1 2 3 4 5 6
$P$ $\frac{1}{64}$ $\frac{3}{32}$ $\frac{15}{64}$ $\frac{5}{16}$ $\frac{15}{64}$ $\frac{3}{32}$ $\frac{1}{64}$
所以$X^{2}$的分布列为
$X^{2}$ 0 1 4 9 16 25 36
$P$ $\frac{1}{64}$ $\frac{3}{32}$ $\frac{15}{64}$ $\frac{5}{16}$ $\frac{15}{64}$ $\frac{3}{32}$ $\frac{1}{64}$
所以$E(X^{2})=1×\frac{3}{32}+4×\frac{15}{64}+9×\frac{5}{16}+16×\frac{15}{64}+25×\frac{3}{32}+36×\frac{1}{64}=\frac{21}{2}$.
7. (教材变式) 某届国际羽联世界锦标赛单打决赛在甲、乙两人之间进行,比赛采用五局三胜制. 按以往比赛经验,每一局甲获胜的概率为 $ p ( 0 < p < 1 ) $,则下列说法一定正确的有
(
A.当 $ p = \frac { 2 } { 3 } $ 时,打四局比赛结束的概率大干打五局比赛结束的概率
B.当 $ p = \frac { 2 } { 3 } $ 时,打三局比赛结束的概率最大
C.当 $ p = \frac { 1 } { 6 } $ 时,打四局比赛结束的概率大于打五局比赛结束的概率
D.当 $ p = \frac { 1 } { 6 } $ 时,打三局比赛结束的概率最大
(
ACD
)A.当 $ p = \frac { 2 } { 3 } $ 时,打四局比赛结束的概率大干打五局比赛结束的概率
B.当 $ p = \frac { 2 } { 3 } $ 时,打三局比赛结束的概率最大
C.当 $ p = \frac { 1 } { 6 } $ 时,打四局比赛结束的概率大于打五局比赛结束的概率
D.当 $ p = \frac { 1 } { 6 } $ 时,打三局比赛结束的概率最大
答案:
7. ACD 当$p=\frac{2}{3}$时,甲输的概率为$\frac{1}{3}$,打四局比赛结束的概率为$\frac{2}{3}C_{3}^{2}×(\frac{2}{3})^{2}×\frac{1}{3}+\frac{1}{3}C_{3}^{3}×(\frac{1}{3})^{3}×\frac{2}{3}=\frac{10}{27}$,打五局比赛结束的概率为$\frac{2}{3}C_{4}^{2}×(\frac{2}{3})^{2}×(\frac{1}{3})^{2}+\frac{1}{3}C_{4}^{3}×(\frac{1}{3})^{3}×(\frac{2}{3})^{2}=\frac{8}{27}$,打三局比赛结束的概率为$(\frac{1}{3})^{3}+(\frac{2}{3})^{3}=\frac{1}{3}$,所以打四局比赛结束的概率大于打五局比赛结束的概率,打三局比赛结束的概率最大,故A正确,B错误;当$p=\frac{1}{6}$时,甲输的概率为$\frac{5}{6}$,打四局比赛结束的概率为$\frac{1}{6}C_{3}^{3}×(\frac{1}{6})^{3}×\frac{5}{6}+\frac{5}{6}C_{3}^{3}×(\frac{5}{6})^{3}×\frac{1}{6}=\frac{65}{216}$,打五局比赛结束的概率为$\frac{1}{6}C_{4}^{2}×(\frac{1}{6})^{2}×(\frac{5}{6})^{2}+\frac{5}{6}C_{4}^{2}×(\frac{5}{6})^{2}×(\frac{1}{6})^{2}=\frac{25}{216}$,打三局比赛结束的概率为$(\frac{1}{6})^{3}+(\frac{5}{6})^{3}=\frac{126}{216}$,所以打四局比赛结束的概率大于打五局比赛结束的概率,打三局比赛结束的概率最大,故C,D正确.
查看更多完整答案,请扫码查看


