《2025年小题狂做高中数学选择性必修第三册人教版》

1. 甲、乙两人下象棋,胜者得 1 分,平局得 0 分,负者得$-1$ 分,共下 5 局.用 $\xi$ 表示甲的得分,则 $\xi=3$ 表示
(D)

A.甲胜 3 局负 2 局
B.甲胜 4 局负 1 局
C.甲胜 3 局平 2 局或甲胜 3 局负 2 局
D.甲胜 4 局负 1 局或甲胜 3 局平 2 局

答案： 1. D 由已知可得，当$\xi=3$时，应该为3胜2平或4胜1负.

2. 袋中装有大小相同的 6 个黑球、5 个白球,从袋中每次任意取出 1 个球且不放回,直到取出白球为止,记所需要的取球次数为随机变量 $X$,则 $X$ 的可能取值为
(B)

A.$1,2,3,·s,6$
B.$1,2,3,·s,7$
C.$0,1,2,·s,5$
D.$1,2,·s,5$

答案： 2. B 因为取到白球时停止，所以最少取球次数为1，即第一次就取到了白球，最多取球次数是7，即把所有的黑球取完之后才取到白球.所以取球次数可以是$1,2,3,·s,7$.

3. 若 $X$ 服从两点分布,且 $P(X=1)-P(X=0)=0. 32$,则 $P(X=0)=$
(B)
A.0. 32
B.0. 34
C.0. 66
D.0. 68

答案： 3. B 依题意可得$P(X=1)+P(X=0)=1$，$P(X=1)-P(X=0)=0.32$，所以$P(X=0)=\frac{1-0.32}{2}=0.34$.

4. 已知随机变量 $X$ 的分布列如表所示,则 $P(|X-3|=1)=$
(B)


A.$\frac{7}{12}$
B.$\frac{5}{12}$
C.$\frac{1}{4}$
D.$\frac{1}{6}$

答案： 4. B 由$|X - 3| = 1$，解得$X=2$或$X=4$. 又$P(X=2)=1-\frac{1}{3}-\frac{1}{4}-\frac{1}{6}=\frac{1}{4}$，所以$P(|X - 3| = 1)=P(X=2)+P(X=4)=\frac{1}{4}+\frac{1}{6}=\frac{5}{12}$.

5. (高频导向 已知盒中有 6 个灯泡,其中 4 正品、2 个次品.从中每次取出 1 个灯泡,取出后不放回,直到取出 2 个正品为止.设 $X$ 为取出的次数,则 $P(X=3)=$
(C)

A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{2}{5}$
D.$\frac{1}{5}$

答案： 5. C 任取三次灯泡所对应的事件总数为$A_{5}^{3}$.要想取出的次数为3时正好停止，只需前面两次取出一正品一次品且第三次取出正品即可，对应的事件个数为$C_{4}^{1}C_{2}^{1}A_{2}^{2}C_{3}^{1}$，所以$P(X=3)=\frac{C_{4}^{1}C_{2}^{1}A_{2}^{2}C_{3}^{1}}{A_{5}^{3}}=\frac{2}{5}$.

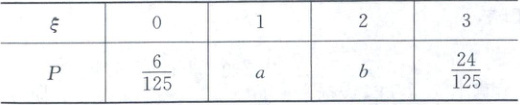
6. 某学生在参加政、史、地三门课程的学业水平考试中,取得 $A$ 等级的概率分别为 $\frac{4}{5},\frac{3}{5},\frac{2}{5}$,且三门课程的成绩是否取得 $A$ 等级相互独立.记 $\xi$ 为该生取得 $A$ 等级的课程数,其分布列如下表所示,则 $a$,$b$ 的值分别为
(C)


A.$\frac{39}{125},\frac{56}{125}$
B.$\frac{56}{126},\frac{39}{125}$
C.$\frac{37}{125},\frac{58}{125}$
D.$\frac{58}{125},\frac{37}{125}$

答案： 6. C 学生在参加政、史、地三门课程的学业水平考试中，有两门取得A等级有以下三种情况：政、史；政、地；地、史.则$P(\xi=2)=\frac{4}{5} × \frac{3}{5} × (1 - \frac{2}{5}) + \frac{4}{5} × (1 - \frac{3}{5}) × \frac{2}{5} + (1 - \frac{4}{5}) × \frac{3}{5} × \frac{2}{5} = \frac{58}{125}$，即$b=\frac{58}{125}$. 根据分布列的性质可得$P(\xi=1)=1 - P(\xi=0) - P(\xi=2) - P(\xi=3)=1 - \frac{6}{125}-\frac{58}{125}-\frac{24}{125}=\frac{37}{125}$，即$a=\frac{37}{125}$.

7. 下列随机变量是离散型随机变量的是
(ACD)

A.掷 5 次硬币,正面向上的次数 $M$
B.某人每天早晨在某公共汽车站等某一路车的时间 $T$
C.从标有数字$1$至$4$的$4$个小球中任取$2$个小球，这$2$个小球上所标的数字之和$Y$
D.将一个骰子掷 3 次,3 次出现的点数之和 $X$

答案： 7. ACD 在 A 中，掷5次硬币正面向上的次数$M$可能取的值，可以按一定次序一一列出，故 A 中的$M$是离散型随机变量；在 B 中，某人每天早晨在某公共汽车站等某一路车的时间$T$可以取某一区间内的一切值，无法按一定次序一一列出，故 B 中的$T$不是离散型随机变量；在 C 中，从标有数字1至4的4个小球中任取2个小球，这2个小球上所标的数字之和$Y$可能取的值，可以按一定次序一一列出，故 C 中的$Y$是离散型随机变量；在 D 中，将一个骰子掷3次，3次出现的点数之和$X$可能取的值，可以按一定次序一一列出，故 D 中的$X$是离散型随机变量.