《2025年小题狂做高中数学选择性必修第三册人教版》

1. [2025 浙江温州期末]一个袋子中有除颜色外完全相同的$x$个红球、3个白球.若采取
不放回的方式从中随机摸出两个球,则摸出的 2 个球都是红球的概率是$\frac {1}{10}$.现采取有
放回的方式从中依次摸出 3 个球,则恰有两次摸出红球的概率为
(A)

A.$\frac {36}{125}$
B.$\frac {12}{125}$
C.$\frac {12}{25}$
D.$\frac {4}{25}$

答案： 1.A 根据题意，不放回地摸出2个球都是红球的概率为
$P_1=\frac{C_x^2}{C_{x+3}^2}=\frac{x(x - 1)}{(x + 3)(x + 2)}=\frac{1}{10}$，即$9x^2 - 15x - 6 = 0$，解得$x = 2$（舍去负根）.所以若有放回地摸球，则每次摸出红球的概率为$\frac{2}{5}$，摸出白球的概率为$\frac{3}{5}$，所以在三次摸球中，恰好有两次摸出红球的概率为$P_2 = C_3^2×(\frac{2}{5})^2×\frac{3}{5}=\frac{36}{125}$.

2. [2025 河北石家庄期末]一个箱子中有 100 个除颜色外完全相同的球,其中有 40 个黄
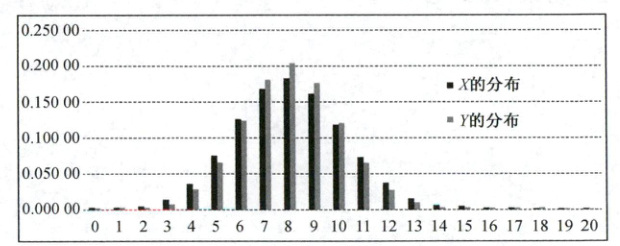
球、60 个红球,从中随机地摸出 20 个,用$X$表示有放回地摸球时摸到黄球的个数,用$Y$
表示不放回地摸球时摸到的黄球个数,$X,Y$的概率分布图如图所示,则下列结论正确
的是
(A)


A.$D(X)＞D(Y)$
B.$D(X)＜D(Y)$
C.$E(X)＞E(Y)$
D.$E(X)＜E(Y)$

答案： 2.A 由题意可知X服从二项分布，Y服从超几何分布，因此它们的期望相同，又因为由图可知Y的分布更集中在均值附近，所以$D(X)＞D(Y)$.

3. [2024 河北保定期中]抛掷一枚质地均匀的硬币,记$a_n=\begin{cases} 1,第n次正面向上, \\ -1,第n次反面向上. \end{cases}$ $S_n$为
数列$\{a_n\}$的前$n$项和,则$\vert S_3\vert=1$且$S_{10}=4$的概率为
(B)

A.$\frac {9}{256}$
B.$\frac {21}{256}$
C.$\frac {3}{128}$
D.$\frac {13}{128}$

答案： 3.B 由题意知，满足$\vert S_3\vert = 1$且$S_{10}=4$有如下两种情况：
①当$S_3 = 1$时，前3次中出现2次正面向上、1次反面向上，后面7次中出现5次正面向上、2次反面向上，其概率为
$p_1 = C_3^2×(\frac{1}{2})^2×(\frac{1}{2})× C_7^5×(\frac{1}{2})^5×(\frac{1}{2})^2=\frac{63}{1024}$；②当
$S_3 = - 1$时，前3次中出现1次正面向上2次反面向上，后面7次中出现6次正面向上1次反面向上，其概率为$p_2 = C_3^1×(\frac{1}{2})×(\frac{1}{2})^2× C_7^6×(\frac{1}{2})^6×(\frac{1}{2})=\frac{21}{1024}$.所以$\vert S_3\vert = 1$且$S_{10}=4$的概率为$p = p_1 + p_2=\frac{63}{1024}+\frac{21}{1024}=\frac{21}{256}$.

4. [多选题][2025 浙江浙南名校期中]已知袋中有除颜色外其他都相同的小球共 9 个,其
中黑球 6 个、红球 3 个,从中摸 4 个球.方案一:有放回地摸球,记取得红球的个数为$X$;
方案二:不放回地摸球,记取得红球的个数为$Y$.下列说法正确的有
(ACD)

A.$P(X\geq1)=\frac {65}{81}$
B.$P(X=i)＜P(Y=i)$,其中$i=0,1,2,3$
C.$E(X)=E(Y)$
D.$D(X)＞D(Y)$

答案： 4.ACD 对于A，方案一中每次摸到红球的概率为$\frac{3}{9}=\frac{1}{3}$，
摸4次球，则取得红球个数$X\sim B(4,\frac{1}{3})$，所以$P(X\geq1)=1 - P(X = 0)=1 - C_4^0×(\frac{1}{3})^0×(1 - \frac{1}{3})^4=\frac{65}{81}$，故A正确；
对于B，方案一中，$P(X = i)=C_4^i(\frac{1}{3})^i(1 - \frac{1}{3})^{4 - i}=C_4^i(\frac{1}{3})^i(\frac{2}{3})^{4 - i}$，$i = 0,1,2,3$，方案二中取得红球的个数Y
服从超几何分布，则$P(Y = i)=\frac{C_i^iC_6^{4 - i}}{C_9^4}$，$i = 0,1,2,3$，当$i = 0$
时，$P(X = 0)=(\frac{2}{3})^4=\frac{16}{81}$，$P(Y = 0)=\frac{C_6^4}{C_9^4}=\frac{224}{1134}$，$P(X = 0)＞P(Y = 0)$，故B错误；对于C，
$E(X)=4×\frac{1}{3}=\frac{4}{3}$，$E(Y)=4×\frac{3}{9}=\frac{4}{3}$，所以$E(X)=$
$E(Y)$，故C正确；对于D，$D(X)=np(1 - p)=4×\frac{1}{3}×(1 - \frac{1}{3})=\frac{8}{9}$，$D(Y)=n·\frac{M}{N}·(1 - \frac{M}{N})·\frac{N - n}{N - 1}=4×\frac{3}{9}×(1 - \frac{3}{9})×\frac{9 - 4}{9 - 1}=\frac{5}{9}$，即$D(X)＞D(Y)$，故D正确.
方法总结 有放回抽取是二项分布，无放回抽取是超几何分布.

5. [2025 江西抚州质量监测]甲、乙两人玩掷六面骰游戏,各个面的点数分别为 1~6. 两人
各投掷一次,当两人的骰子向上的点数之差为偶数时,视为平局,当两人的骰子向上的
点数之差为奇数时,谁的点数大谁胜……重复上面的步骤,游戏进行到一方比对方多
胜 2 次或平局 4 次时停止,记游戏停止时游戏的局数为$X$,则$P(X=4)=$$\frac{11}{64}$.

答案： 5.$\frac{11}{64}$ 甲、乙各掷骰子1次，若两人的点数都是偶数或都是奇数，则平局，所以平局的概率为$p_1=\frac{2×3×3}{6×6}=\frac{1}{2}$；若甲
胜，则结果有$(2,1),(3,2),(4,1),(4,3),(5,2),(5,4),(6,1),(6,3),(6,5)$，9种，所以甲胜的概率为$p_2=\frac{9}{6×6}=\frac{1}{4}$；
同理，乙胜的概率也为$\frac{1}{4}$.停止游戏时局数为4，若4局全是
平局，则其概率为$(\frac{1}{2})^4=\frac{1}{16}$；若平局2次，则最后1局不能
是平局，且另外2局甲全胜或乙全胜，其概率为$C_3^2×(\frac{1}{4})^2×\frac{1}{2}×\frac{1}{2}×2=\frac{3}{32}$；若平局0次，则一方3胜1负，且负的1局
只能在前2局中，其概率为$C_2^1×\frac{1}{4}×(\frac{1}{4})^3×2=\frac{1}{64}$.所以
$P(X = 4)=\frac{1}{16}+\frac{3}{32}+\frac{1}{64}+\frac{1}{64}=\frac{11}{64}$.