《2025年小题狂做高中数学选择性必修第三册人教版》

1. [2024 全国甲卷文,4]甲、乙、丙、丁四人排成一列，则丙不在排头，且甲或乙在排尾的概率是
(B)

A.$\frac {1}{4}$
B.$\frac {1}{3}$
C.$\frac {1}{2}$
D.$\frac {2}{3}$

答案：
1. B 解法1 画出树状图，如图：
　　
由树状图可得，甲、乙、丙、丁四人排成一列，共有24种排法，其中丙不在排头，且甲或乙在排尾的排法共有8种，故所求概率为$\frac{8}{24}=\frac{1}{3}$.
解法2 当甲排在排尾，乙排第一位时，丙、丁任意排列在第二、三位上，共2种；当甲排在排尾，乙排第二位或第三位时，丙有1种排法，丁排在排头，共2种.故甲排在排尾共有4种方法，同理，乙排在排尾共有4种方法，共8种排法符合题意.基本事件总数为$A_4^4 = 24$，根据古典概型的计算公式，丙不在排头，甲或乙在排尾的概率为$\frac{8}{24}=\frac{1}{3}$.

2. [2023 全国甲卷文,4]某校文艺部有 4 名学生，其中高一、高二年级各占 2 名.从这 4 名学生中随机选 2 名组织校文艺汇演，则这 2 名学生来自不同年级的概率为
(D)

A.$\frac {1}{6}$
B.$\frac {1}{3}$
C.$\frac {1}{2}$
D.$\frac {2}{3}$

答案： 2. D 依题意，从这4名学生中随机选2名组织校文艺汇演，总的基本事件有$C_4^2 = 6$（件），其中这2名学生来自不同年级的基本事件有$C_2^1C_2^1 = 4$（件），所以这2名学生来自不同年级的概率为$\frac{4}{6}=\frac{2}{3}$.

3. [2022 新高考Ⅱ卷,5]有甲、乙、丙、丁、戊 5 名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同排列方式共有
(B)

A.12 种
B.24 种
C.36 种
D.48 种

答案： 3. B 因为丙、丁要在一起，所以先把丙、丁捆绑，看作一个元素，连同乙、戊看成三个元素排列，有$A_3^3$种排列方式.甲不站在两端，只需甲在此三个元素的中间两个位置中任选一个插入，有2种插空方式.注意到丙、丁两人的顺序可交换，有2种排列方式，故这5名同学共有$A_3^3×2×2 = 24$（种）不同的排列方式.

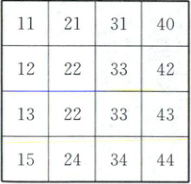
4. [2024 新高考Ⅱ卷,14]在如图的 4×4 的方格表中选 4 个方格，要求每行和每列均恰有一个方格被选中，则共有24种选法，在所有符合上述要求的选法中，选中的方格中的 4 个数之和的最大值是112.

答案： 4. 24 112 由题意知，第一列有4个方格可选，第二列有3个方格可选，第三列有2个方格可选，第四列有1个方格可选，所以共有$4×3×2×1 = 24$（种）选法.每种选法可标记为$(a,b,c,d)$，$a,b,c,d$分别表示第一、二、三、四列的数字，则所有的可能结果为$(11,22,33,44)$，$(11,22,34,43)$，$(11,22,33,44)$，$(11,22,34,42)$，$(11,24,33,43)$，$(11,24,33,42)$，$(12,21,33,44)$，$(12,21,34,43)$，$(12,22,31,44)$，$(12,22,34,40)$，$(12,24,31,43)$，$(12,24,33,40)$，$(13,21,33,44)$，$(13,21,34,42)$，$(13,22,31,44)$，$(13,24,34,40)$，$(13,24,31,42)$，$(13,24,33,40)$，$(15,21,33,43)$，$(15,21,33,42)$，$(15,22,31,43)$，$(15,22,33,40)$，$(15,22,31,42)$，$(15,22,33,40)$，所以$(15,21,33,43)$这4个数之和最大，为$15 + 21 + 33 + 43 = 112$.

5. [2024 全国甲卷理,13] $(\frac {1}{3}+x)^{10}$ 的展开式中，各项系数中的最大值为5.

答案： 5. 5 由题知展开式的通项为$T_{r + 1} = C_{10}^r(\frac{1}{3})^{10 - r}x^r$，$0\leq r\leq10$且$r\in Z$，设展开式中第$(r + 1)$项的系数最大，则$\begin{cases}C_{10}^r(\frac{1}{3})^{10 - r}\geq C_{10}^{r + 1}(\frac{1}{3})^{9 - r},\\C_{10}^r(\frac{1}{3})^{10 - r}\geq C_{10}^{r - 1}(\frac{1}{3})^{11 - r},\end{cases}$解得$\frac{29}{4}\leq r\leq\frac{33}{4}$.又$r\in Z$，所以$r = 8$，所以展开式中系数最大的项是第9项，且该项系数为$C_{10}^8(\frac{1}{3})^2 = 5$.

6. [2025 天津卷,11]在$(x - 1)^6$的展开式中,$x^3$的系数为-20.

答案： 6. -20 $(x - 1)^6$展开式的通项为$T_{r + 1} = C_6^rx^{6 - r}·(-1)^r$，当$r = 3$时，$T_4 = C_6^3x^3·(-1)^3 = -20x^3$，即$(x - 1)^6$展开式中$x^3$的系数为-20.

7. [2023 新高考Ⅰ卷,13]某学校开设了 4 门体育类选修课和 4 门艺术类选修课，学生需从这 8 门课中选修 2 门或 3 门课，并且每类选修课至少选修 1 门，则不同的选课方案共有64种(用数字作答).

答案： 7. 64 从8门课中选修2门，则不同的选课方案共有$C_8^2 = 16$（种）.从8门课中选修3门，①若体育类选修1门，则不同的选课方案共有$C_4^1C_4^2 = 24$（种）；②若体育类选修2门，则不同的选课方案共有$C_2^2C_4^1 = 24$（种）.综上所述，不同的选课方案共有$16 + 24 + 24 = 64$（种）.

8. [2022 新高考Ⅰ卷,13] $\left(1 - \frac{y}{x}\right)(x + y)^8$ 的展开式中$x^2 y^6$的系数为-28(用数字作答).

答案： 8. -28 因为$(1 - \frac{y}{x})(x + y)^8 = (x + y)^8 - \frac{y}{x}(x + y)^8$，所以$(1 - \frac{y}{x})(x + y)^8$的展开式中含$x^2y^6$的项为$C_8^5x^5y^3 - \frac{y}{x}C_8^6x^6y^2 = - 28x^2y^6$，即$(1 - \frac{y}{x})(x + y)^8$的展开式中，$x^2y^6$的系数为-28.

9. [2025 北京卷,12]已知$(1 - 2x)^4 = a_0 - 2a_1x + 4a_2x^2 - 8a_3x^3 + 16a_4x^4$，则$a_0 =$1;$a_1 + a_2 + a_3 + a_4 =$15.

答案： 9. 1 15 令$x = 0$，则$a_0 = 1$.由题可知$(1 - 2x)^4 = a_0 + a_1(-2x) + a_2(-2x)^2 + a_3(-2x)^3 + a_4(-2x)^4$，令$t = -2x$，则$(1 + t)^4 = a_0 + a_1t + a_2t^2 + a_3t^3 + a_4t^4$，令$t = 1$，则$a_0 + a_1 + a_2 + a_3 + a_4 = 2^4$，故$a_1 + a_2 + a_3 + a_4 = 15$.