《2025年小题狂做高中数学选择性必修第三册人教版》

8. 随机地向4个器皿内投放4种不同的食物给4只狗仔喂食，设所投放的食物均落在器皿内，随机变量$X$为空器皿的个数，则下列说法正确的是
(CD)

A. 随机变量$X$的可能取值为1,2,3
B. $P(X=2)=\frac{9}{64}$
C. $P(X=3)=\frac{1}{64}$
D. $E(X)=\frac{81}{64}$

答案： 8.CD 由题意得随机变量$X$的可能取值为$0,1,2,3$，故A
错误；$P(X=2)=\frac{C_{4}^{2}C_{2}^{2}}{A_{2}^{2}} × \frac{A_{2}^{2}}{4^{4}}=\frac{21}{64}$，$P(X=3)=\frac{C_{4}^{1}}{4^{4}}=\frac{1}{64}$，
故B错误，C正确；又$P(X=1)=\frac{C_{2}^{2}A_{3}^{3}}{4^{4}}=\frac{9}{16}$，$P(X=0)=$
$\frac{A_{4}^{4}}{4^{4}}=\frac{3}{32}$，所以$E(X)=3 × \frac{1}{64}+2 × \frac{21}{64}+1 × \frac{9}{16}+0 × \frac{3}{32}=\frac{81}{64}$，
故D正确.

9. 小张上班从家到公司开车有两条线路，所需时间(分钟)随交通堵塞状况不同而有所变化，其概率分布如下表所示.

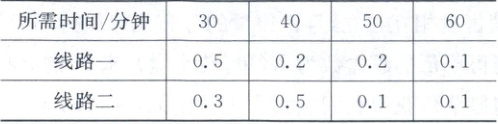
则下列说法正确的是
(BD)

A. 任选一条线路，“所需时间小于50分钟”与“所需时间为60分钟”是对立事件
B. 从所需的平均时间看，线路一比线路二更节省时间
C. 如果要求在45分钟以内从家赶到公司，小张应该走线路一
D. 若小张上、下班走不同线路，则所需时间之和大于100分钟的概率为0.04

答案： 9.BD 对于A，“所需时间小于50分钟”与“所需时间为60
分钟”是互斥事件而不是对立事件，故A错误；对于B，线路
一所需的平均时间为$30 × 0.5+40 × 0.2+50 × 0.2+60 ×$
$0.1=39$（分钟），线路二所需的平均时间为$30 × 0.3+40 ×$
$0.5+50 × 0.1+60 × 0.1=40$（分钟），所以线路一比线路二
更节省时间，故B正确；对于C，线路一所需时间在45分钟
内的概率为$0.7$，线路二所需时间在45分钟内的概率为
$0.8$，小张应该选线路二，故C错误；对于D，所需时间之和
大于100分钟，则线路一、线路二的时间可以为$(50,60)$，$(60,$
$50)$和$(60,60)$三种情况，概率为$0.2 × 0.1+0.1 × 0.1+$
$0.1 × 0.1=0.04$，故D正确.

10. (教材变式)在单项选择题中，每道题有4个选项，其中仅有一个选项是正确的，如果从四个选项中随机选一个，选对的概率为0.25，为了减少随机选择也得分的影响，某次考试单项选择题采用选错扣分的规则，选对得3分，选错扣$a$分.若随机选择时得分的均值为0分，则$a=$1.

答案： 10.1 由$0.25 × 3+(1-0.25)(-a)=0$，得$a=1$.
教材链接（选择性必修三习题7.3第4题改编）

11. 编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的个数是$\xi$，则$E(\xi)=$1.

答案： 11.1 因为编号为1,2,3的三位学生随意入座编号为1,2,
3的3个座位，所以有123,132,213,231,312,321，共6种结
果.设与座位编号相同的学生个数为$\xi$，则$\xi$的可能取值为
$0,1,3$，所以$\xi$的分布列为
$\begin{array}{c|ccc}\xi & 0 & 1 & 3 \\ \hline P & \frac{1}{3} & \frac{1}{2} & \frac{1}{6} \end{array}$
所以$E(\xi)=0 × \frac{1}{3}+1 × \frac{1}{2}+3 × \frac{1}{6}=1$.

12. 甲、乙两人进行乒乓球比赛，每人每局取胜的概率均为$\frac{1}{2}$，现采用五局三胜制，胜3局者赢得全部奖金800元.若前两局比赛均为甲胜，此时因某种原因比赛中止，为使奖金分配合理，则乙应得奖金100元.

答案： 12.100 设正常比赛甲可得奖金为$X$，$X$的可能取值为
$800,0$.甲赢得比赛有3种情况：①胜第3局，甲赢的概率为
$\frac{1}{2}$；②输第3局，胜第4局，甲赢的概率为$\frac{1}{2} × \frac{1}{2}=\frac{1}{4}$；③输
第3,4局，胜第5局，甲赢的概率为$\frac{1}{2} × \frac{1}{2} × \frac{1}{2}=\frac{1}{8}$.所以
甲赢的概率为$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{7}{8}$，因此$E(X)=800 × \frac{7}{8}+$
$0 × \frac{1}{8}=700$，所以乙应得奖金$800-700=100$（元）.

13. (教材变式)某厂销售部以箱为单位销售某种零件，每箱的定价为200元，低于100箱按原价销售，不低于100箱则有以下两种优惠方案：
①以100箱为基准，每多50箱送5箱；
②通过双方议价，买方能以优惠8％成交的概率为0.6，以优惠6％成交的概率为0.4.
某单位需要这种零件650箱，以购买总价的数学期望为决策依据，试问该单位选择哪种优惠方案更划算？

答案： 13.解：若选择方案①，则购买600箱能获赠50箱，从而购买
总价为$200 × 600=$
$120000$（元）.
若选择方案②，设在折扣优惠中每箱零件的价格为$X$元，则
$X$的可能取值为$184,188$.$X$的分布列为
$\begin{array}{c|cc}X & 184 & 188 \\ \hline P & 0.6 & 0.4 \end{array}$
则在折扣优惠中每箱零件价格的数学期望$E(X)=184 ×$
$0.6+188 × 0.4=185.6$.
则购买总价的数学期望为$185.6 × 650=120640$（元）.
因为$120640＞120000$，所以选择方案①更划算.
教材链接（选择性必修三7.3.1例4改编）