《2025年小题狂做高中数学选择性必修第三册人教版》

1. $C_{6}^{0}+C_{6}^{1}+C_{6}^{2}+C_{6}^{3}+C_{6}^{4}+C_{6}^{5}=$

A.64
B.63
C.62
D.61

答案： 1. B 因为$C_{6}^{0}+C_{6}^{1}+C_{6}^{2}+C_{6}^{3}+C_{6}^{4}+C_{6}^{5}+C_{6}^{6}=2^{6}$，所以原式$=2^{6}-1=63$.

2. 在$(x+1)^{n}$的展开式中，只有第 5 项的二项式系数最大，则正整数$n=$

A.7
B.8
C.9
D.10

答案： 2. B 由题意，得$(x+1)^{n}$的展开式共有$9$项，即$n+1=9$，所以$n=8$.

3. 设二项式$(\sqrt[3]{x}+\frac{3}{x})^{n}$的展开式中各项系数的和为$a$，所有二项式系数的和为$b$. 若$a+2b=80$，则$n$的值为

A.8
B.4
C.2
D.3

答案： 3. D 在二项式$(\sqrt[3]{x}+\frac{3}{x})^{n}$的展开式中，令$x=1$，得展开式的各项系数之和$a=4^{n}$.由二项式系数的性质，得二项式系数的和$b=2^{n}$.由$a+2b=80$，得$4^{n}+2×2^{n}=80$，解得$n=3$.

4. 在$(x-2\sqrt{x}+1)^{3}$的展开式中，含$x^{2}$的项的系数为

A.20
B.15
C.6
D.3

答案： 4. B 由题$(x - 2\sqrt{x}+1)^{3}=[(\sqrt{x})^{2}-2\sqrt{x}+1]^{3}=(\sqrt{x}-1)^{6}$，其中$(\sqrt{x}-1)^{6}$展开式的通项为$T_{r + 1}=(-1)^{r}·$
$C_{6}^{r}(\sqrt{x})^{6 - r}=(-1)^{r}· C_{6}^{r}x^{\frac{6 - r}{2}}(0\leq r\leq6$且$r\in\mathbf{N})$.令$\frac{6 - r}{2}=2$，解得$r = 2$，所以$T_{3}=(-1)^{2}· C_{6}^{2}x^{2}=15x^{2}$，即$(x - 2\sqrt{x}+1)^{3}$的展开式中含$x^{2}$的项的系数为$15$.

5. 已知$(x-1)^{4}(x^{2}-2x+2)=a_{0}+a_{1}x+a_{2}x^{2}+·s+a_{6}x^{6}$，则$a_{2}-a_{0}=$

A.20
B.19
C.-8
D.-15

答案： 5. B 因为$(x - 1)^{4}(x^{2}-2x + 2)=(x - 1)^{6}+(x - 1)^{4}$，所以$a_{2}=C_{6}^{2}+C_{4}^{2}=21$，$a_{0}=2$，则$a_{2}-a_{0}=19$.

6. 已知$(2+x)+(2+x)^{2}+·s+(2+x)^{10}=a_{0}+a_{1}(1+x)+·s+a_{10}(1+x)^{10}(x\neq-2,x\neq-1)$，则$a_{3}=$

A.210
B.330
C.165
D.145

答案： 6. B 令$t = 1 + x$，则$(1 + t)+(1 + t)^{2}+·s+(1 + t)^{10}=a_{0}+a_{1}t+·s+a_{10}t^{10}$，所以$a_{0}+a_{1}t+·s+a_{10}t^{10}=(1 + t)+(1 + t)^{2}+·s+(1 + t)^{10}=\frac{(1 + t)^{11}-(1 + t)}{t}$，即$a_{0}t+a_{1}t^{2}+a_{2}t^{3}+a_{3}t^{4}+·s+a_{10}t^{11}=(1 + t)^{11}-t - 1$，所以$a_{3}$是$(1 + t)^{11}-t - 1$中$t^{4}$的系数，而$(1 + t)^{11}-t - 1=\sum_{k = 0}^{11}C_{11}^{k}t^{k}-t - 1$，所以$a_{3}=C_{11}^{4}=\frac{11×10×9×8}{4×3×2×1}=330$.

7. 高频导向 关于多项式$(x-\frac{1}{x^{2}}+2)$的展开式，下列说法正确的是

A.常数项为-88
B.含$x^{2}$的项的系数为 80
C.展开式的系数和为 32
D.展开式中存在含$x^{-9}$的项

答案： 7. AC $(x-\frac{1}{x^{2}}+2)^{5}$中取$2$个$x$，$1$个$-\frac{1}{x^{2}}$，$2$个$2$，乘在一起为常数项，或是$5$个$2$相乘也是常数项，所以展开式中常数项为$C_{5}^{2}× C_{3}^{1}×(-1)^{1}× C_{2}^{2}×2^{2}+2^{5}=-88$，故A正确；$(x-\frac{1}{x^{2}}+2)^{5}$中取$4$个$x$，$1$个$-\frac{1}{x^{2}}$，相乘在一起得到含$x^{2}$的项，或是$2$个$x$，$3$个$2$相乘在一起得到含$x^{2}$的项，所以展开式中$x^{2}$项为$C_{5}^{4}× C_{1}^{1}×(-1)^{1}+C_{5}^{2}× C_{3}^{3}×2^{3}=75$，故B错误；令$x = 1$，展开式的系数和为$2^{5}=32$，故C正确；由题很显然不可能凑成$x^{-9}$，故D错误.

8. 已知$(2x-1)^{7}=a_{0}+a_{1}(x-1)+a_{2}(x-1)^{2}+·s+a_{6}(x-1)^{6}+a_{7}(x-1)^{7}$，则

A.$a_{0}=1$
B.$a_{1}+a_{2}+a_{3}+·s+a_{7}=3^{7}-1$
C.$a_{5}=-672$
D.$\frac{a_{1}}{2}+\frac{a_{2}}{2^{2}}+\frac{a_{3}}{2^{3}}+·s+\frac{a_{7}}{2^{7}}=127$

答案： 8. ABD 对于A，令$x = 1$，可得$a_{0}=(2 - 1)^{7}=1$，故A正确；对于B，令$x = 2$，$a_{0}+a_{1}+a_{2}+·s+a_{6}+a_{7}=(4 - 1)^{7}=3^{7}$，所以$a_{1}+a_{2}+·s+a_{6}+a_{7}=3^{7}-a_{0}=3^{7}-1$，故B正确；对于C，$[1 + 2(x - 1)]^{7}=a_{0}+a_{1}(x - 1)+a_{2}(x - 1)^{2}+·s+a_{6}(x - 1)^{6}+a_{7}(x - 1)^{7}$，则$T_{6}=T_{7 - 1}=C_{7}^{5}×1^{2}[2(x - 1)]^{5}=672(x - 1)^{5}$，所以$a_{5}=672$，故C错误；对于D，令$x=\frac{3}{2}$，可得$(2×\frac{3}{2}-1)=a_{0}+a_{1}(\frac{3}{2}-1)+a_{2}(\frac{3}{2}-1)^{2}+·s+a_{6}(\frac{3}{2}-1)^{6}+a_{7}(\frac{3}{2}-1)^{7}$，所以$a_{0}+\frac{a_{1}}{2}+\frac{a_{2}}{2^{2}}+\frac{a_{3}}{2^{3}}+·s+\frac{a_{7}}{2^{7}}=2^{7}=128$，所以$\frac{a_{1}}{2}+\frac{a_{2}}{2^{2}}+\frac{a_{3}}{2^{3}}+·s+\frac{a_{7}}{2^{7}}=128 - 1=127$，故D正确.

9. 创新·新情境“杨辉三角”是中国古代数学文化的瑰宝之一，最早出现在南宋数学家杨辉于 1261 年所著的《详解九章算法》一书中. “杨辉三角”揭示了二项式系数在三角形数表中的一种几何排列规律，如图所示，下列关于“杨辉三角”的结论正确的是



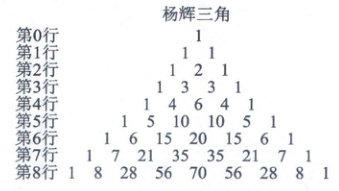
A.$C_{3}^{0}+C_{3}^{3}+·s+C_{5}^{5}=210$
B.第 2025 行中从左往右右第 1011 个数与第 1012 个数相等
C.记第$n$行的第$i$个数为$a_{i}$，则$\sum_{i=1}^{n+1}3^{i-1}a_{i}=4^{n}$
D.第 20 行中第 12 个数与第 13 个数之比为$4:3$

答案： 9. CD 对于A，$C_{5}^{3}+C_{5}^{4}+·s+C_{5}^{5}=C_{5}^{4}+C_{5}^{5}+·s+C_{5}^{3}-C_{5}^{3}=C_{5}^{4}+·s+C_{5}^{3}-C_{5}^{3}=C_{5}^{4}+C_{5}^{3}-C_{5}^{4}=C_{5}^{3}-C_{5}^{4}=10 - 5 = 5$，$C_{6}^{3}+·s+C_{6}^{6}-C_{6}^{4}=C_{6}^{3}+·s+C_{6}^{6}-C_{6}^{4}=C_{7}^{4}-C_{6}^{4}=209$，故A错误；对于B，第$2025$行中的数为$(x + 1)^{2024}$的展开式的二项式系数，则从左往右第$1011$个数为$C_{2024}^{1010}$，第$1012$个数为$C_{2024}^{1011}$，$C_{2024}^{1010}\neq C_{2024}^{1011}$，故B错误；对于C，第$n$行的第$i$个数为$a_{i}=C_{n - 1}^{i - 1}$，则$\sum_{i = 1}^{n + 1}3^{i - 1}a_{i}=\sum_{i = 1}^{n + 1}3^{i - 1}C_{n - 1}^{i - 1}=3^{0}C_{n - 1}^{0}+3^{1}C_{n - 1}^{1}+3^{2}C_{n - 1}^{2}+·s+3^{n}C_{n - 1}^{n - 1}=(1 + 3)^{n - 1}=4^{n - 1}$，故C正确；对于D，第$20$行中的数为$(x + 1)^{19}$的展开式的二项式系数，则从左往右第$12$个数为$C_{19}^{11}$，第$13$个数为$C_{19}^{12}$，则$\frac{C_{19}^{11}}{C_{19}^{12}}=\frac{A_{19}^{11}}{C_{19}^{12}A_{8}^{8}}=\frac{20×19×·s×12×8!}{9!}=\frac{12}{9}=\frac{4}{3}$，故D正确.