《2025年名校课堂七年级数学上册北师大版江西专版》

1. 蟑螂对我们来说是非常熟悉的,它之所以被称为打不死的小强,是因为它的繁殖速度非常惊人. 某种蟑螂繁衍后代的数量为上一代数量的 11 倍,也就是说,如果它的始祖(第一代)有 11 只,那么下一代就会有 121 只,以此类推,这种蟑螂第 15 代的只数是(D)

A.$11^{12}$
B.$11^{13}$
C.$11^{14}$
D.$11^{15}$

答案： D

2. 将正整数按如图所示的位置顺序排列,根据排列规律,则 2 025 应在(D)


A.A 位置
B.B 位置
C.C 位置
D.D 位置

答案： D

3. 小王利用计算机设计了一个计算程序,请根据数据完成下表:

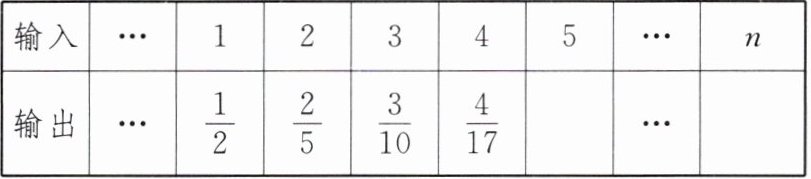
答案： $\frac{5}{26}$　$\frac{n}{n^2+1}$

4. 如图,下列是由同种型号的黑、白两种颜色的等边三角形瓷砖按一定规律铺设的图形. 仔细观察图形可知:
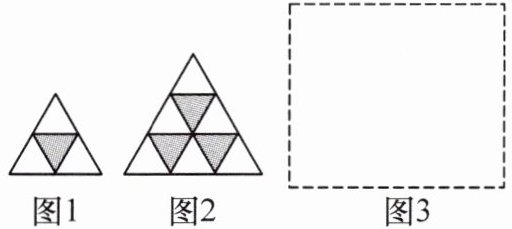
图 1 有 1 块黑色的瓷砖,可表示为 $1=\frac{(1 + 1)×1}{2}$; 图 2 有 3 块黑色的瓷砖,可表示为 $1 + 2=\frac{(1 + 2)×2}{2}$;
实践与探索:
(1)请在图 3 的虚线框内画出第 3 个图形.
(2)第 4 个图形有10块黑色的瓷砖.
(3)第 $n$ 个图形有$\frac{1}{2}n(n+1)$块黑色的瓷砖(用含有 $n$ 的代数式表示).

答案： 解:
(1)图3如图略.
(2)10　
(3)$\frac{1}{2}n(n+1)$

5. (教材 P102 习题 T1 变式)观察:
$2^{1}-1 = 1$, $2^{2}-1 = 3$, $2^{3}-1 = 7$, $2^{4}-1 = 15$, $2^{5}-1 = 31$, $2^{6}-1 = 63$, $2^{7}-1 = 127$, $2^{8}-1 = 255$,……
(1)归纳计算结果中的个位数字的规律.
(2)写出其中个位数字分别为 1,3,7,5 的算式各两个.
(3)指出 $2^{100}-1$ 的个位数字.

答案： 解:
(1)个位数字的规律为1,3,7,5四个数字循环.
(2)$2^9 - 1 = 511$，$2^{10} - 1 = 1023$，$2^{11} - 1 = 2047$，$2^{12} - 1 = 4095$，$2^{13} - 1 = 8191$，$2^{14} - 1 = 16383$，$2^{15} - 1 = 32767$，$2^{16} - 1 = 65535$.(答案不唯一)
(3)
∵$100÷4 = 25$，
∴$2^{100} - 1$的个位数字与$2^4 - 1$的个位数字相同，为5.

6. 探索规律是深入认识事物的一种方法,通过观察、归纳、猜想、验证等思维方式,历经从具体到抽象的过程来揭示一般规律.
问题情景:如图 1,把火柴棒搭成正方形.
(1)问题提出:①按图 1 的方式,搭 4 个正方形需要13根火柴棒.
②其学生是按照图 2 思考的,根据他思考的方法求出搭 $x$ 个正方形所需火柴棒根数的代数式.
(2)问题解决:你还有其他的思考方法得到正方形的个数 $x$ 与火柴棒的根数之间的关系吗? 说明思考方法,画出对应图形,并求出代数式.
(3)问题运用:改变火柴棒的摆放方法搭成别的图形,画出图形,求出图形个数 $a$ 与火柴

棒

根

数之间关系的代数式.

答案：
解:
(1)①13　②搭1个正方形需要4根，搭2个正方形需要火柴棒$4 + 3 = 7$(根)，搭3个正方形需要火柴棒$4 + 3×2 = 10$(根)，搭4个正方形需要火柴棒$4 + 3×3 = 13$(根)，……
∴搭$x$个正方形所需火柴棒的根数为$4 + 3(x - 1) = (3x + 1)$根.
(2)如图，
　　　　　 　　　
搭1个正方形需要火柴棒$(4×1 - 0)$根，搭2个正方形需要火柴棒$(4×2 - 1)$根，搭3个正方形需要火柴棒$(4×3 - 2)$根，……
∴搭$x$个正方形所需火柴棒的根数为$4x - (x - 1) = (3x + 1)$根.
(3)答案不唯一， 例如:按如图的方式搭出下列图形，
同理可得，第$a$个图形所需火柴棒的根数为$6 + 5(a - 1) = (5a + 1)$根.