第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 下列各式不是单项式的为(
A.3
B.$a$
C.$\frac{b}{a}$
D.$\frac{1}{2}x^{2}y$
C
)A.3
B.$a$
C.$\frac{b}{a}$
D.$\frac{1}{2}x^{2}y$
答案:
C
2. 下列各组单项式中,次数相同的是(
A.$3ab$ 与 $-4xy^{2}$
B.$3\pi$ 与 $a$
C.$-\frac{1}{3}x^{2}y^{2}$ 与 $xy$
D.$a^{3}$ 与 $xy^{2}$
D
)A.$3ab$ 与 $-4xy^{2}$
B.$3\pi$ 与 $a$
C.$-\frac{1}{3}x^{2}y^{2}$ 与 $xy$
D.$a^{3}$ 与 $xy^{2}$
答案:
D
3. (2023·江西)单项式 $-5ab$ 的系数为
-5
.
答案:
-5
4. 新考向 开放性问题 请写出一个含有字母 $a$ 和 $b$,且系数为 $-2$,次数为 $4$ 的单项式:
-2a³b
.
答案:
-2a³b(答案不唯一)
5. 若单项式 $-x^{3}y^{n + 5}$ 的系数是 $m$,次数是 $9$,则 $m + n$ 的值为
0
.
答案:
0
6. 填表:


答案:
| 单项式 | $-2a^5$ | $3h$ | $-xy^2$ | $\pi t^2$ | $-\frac{3vt}{2}$ |
| -- | -- | -- | -- | -- | -- |
| 系数 | $-2$ | $3$ | $-1$ | $\pi$ | $-\frac{3}{2}$ |
| 次数 | $5$ | $1$ | $3$ | $2$ | $2$ |
| -- | -- | -- | -- | -- | -- |
| 系数 | $-2$ | $3$ | $-1$ | $\pi$ | $-\frac{3}{2}$ |
| 次数 | $5$ | $1$ | $3$ | $2$ | $2$ |
7. 下列代数式是多项式的是(
A.$2×10^{5}$
B.$a + 1$
C.$2ab$
D.$-\frac{\pi^{2}x^{2}z}{2}$
B
)A.$2×10^{5}$
B.$a + 1$
C.$2ab$
D.$-\frac{\pi^{2}x^{2}z}{2}$
答案:
B
8. 多项式 $3x^{2} - 2x - 1$ 的各项分别是(
A.$3x^{2}$,$2x$,$1$
B.$3x^{2}$,$-2x$,$1$
C.$-3x^{2}$,$2x$,$-1$
D.$3x^{2}$,$-2x$,$-1$
D
)A.$3x^{2}$,$2x$,$1$
B.$3x^{2}$,$-2x$,$1$
C.$-3x^{2}$,$2x$,$-1$
D.$3x^{2}$,$-2x$,$-1$
答案:
D
9. 新考向 开放性问题 如图所示的是一位同学数学笔记可见的一部分.若要补全这个不完整的代数式,则可以补充的内容是

2x³
.
答案:
答案不唯一,如:2x³
10. (1)如果多项式 $x^{n - 2} - 5x + 2$ 是关于 $x$ 的四次三项式,那么 $n =$
(2)若多项式 $\frac{1}{2}x^{\vert m\vert} - (m - 2)x + 7$ 是关于 $x$ 的二次三项式,则 $m =$
6
.(2)若多项式 $\frac{1}{2}x^{\vert m\vert} - (m - 2)x + 7$ 是关于 $x$ 的二次三项式,则 $m =$
-2
.
答案:
(1)6
(2)-2
(1)6
(2)-2
11. 下列多项式分别有几项?每项的系数和次数分别是多少?
(1) $\frac{1}{3}x^{2}y - x^{3} + 2x^{2}$.
(2) $-\frac{5m^{2}n^{2}}{6} + \pi m^{3} - 5^{2}$.
(1) $\frac{1}{3}x^{2}y - x^{3} + 2x^{2}$.
(2) $-\frac{5m^{2}n^{2}}{6} + \pi m^{3} - 5^{2}$.
答案:
解:
(1)三项.每项的系数分别为$\frac{1}{3},$-1,2;次数分别是3,3,2.
(2)三项.每项的系数分别为$-\frac{5}{6},$π,-25;次数分别是4,3,0.
(1)三项.每项的系数分别为$\frac{1}{3},$-1,2;次数分别是3,3,2.
(2)三项.每项的系数分别为$-\frac{5}{6},$π,-25;次数分别是4,3,0.
12. 下列各式中,不是整式的是(
A.$3x$
B.$\frac{1}{x}$
C.$\frac{xy}{2}$
D.$x - 3y$
B
)A.$3x$
B.$\frac{1}{x}$
C.$\frac{xy}{2}$
D.$x - 3y$
答案:
B
13. 请把下列各式的序号分别填入相应的圈内.
① $1$;② $s = ab$;③ $r$;④ $\frac{4}{3}\pi r^{3}$;⑤ $\frac{2n - 3p}{m}$;⑥ $m(m + n)$;⑦ $\frac{2x + 1}{3}$;⑧ $\frac{2x^{2}}{\pi}$.
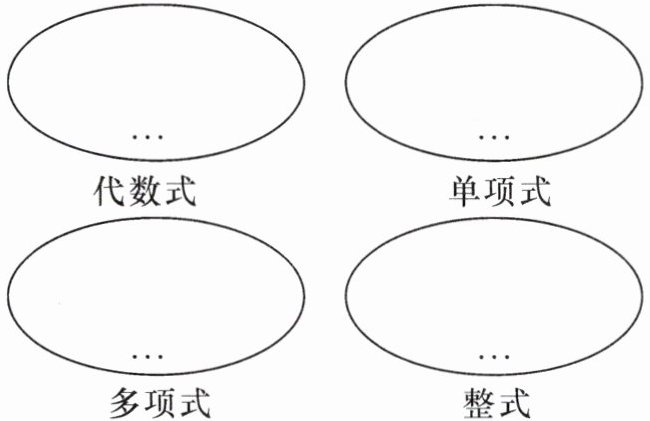
① $1$;② $s = ab$;③ $r$;④ $\frac{4}{3}\pi r^{3}$;⑤ $\frac{2n - 3p}{m}$;⑥ $m(m + n)$;⑦ $\frac{2x + 1}{3}$;⑧ $\frac{2x^{2}}{\pi}$.

答案:
代数式:①③④⑤⑥⑦⑧
单项式:①③④⑧
多项式:⑥⑦
整式:①③④⑥⑦⑧
单项式:①③④⑧
多项式:⑥⑦
整式:①③④⑥⑦⑧
14. (教材 P81“尝试·思考”变式)请列出下列问题中的代数式,并指出其中:①哪些是单项式?单项式的系数和次数分别是多少?②哪些是多项式?多项式的次数是多少?
(1)底面是边长为 $x$ 的正方形,高为 $y$ 的长方体的体积是多少?
(2)目前,在地球上生存的动物约有 $150$ 万种,其中无脊椎动物约有 $m$ 万种,则脊椎动物约有多少万种?
(3)某品牌新能源汽车为了提高市场占有率,将原价为 $a$ 万元/辆的汽车按九折出售.如果一周内这种汽车销售了 $b$ 辆,那么这周的销售额为多少万元?
(4)如图所示的是某古城墙及门洞的示意图,其中门洞的下部是长方形,上部是半圆形,它的面积是多少?若城墙上面的垛口都可看作长为 $a$,宽为 $b$ 的长方形,则每个垛口的面积是多少?
 ]
]
(1)底面是边长为 $x$ 的正方形,高为 $y$ 的长方体的体积是多少?
(2)目前,在地球上生存的动物约有 $150$ 万种,其中无脊椎动物约有 $m$ 万种,则脊椎动物约有多少万种?
(3)某品牌新能源汽车为了提高市场占有率,将原价为 $a$ 万元/辆的汽车按九折出售.如果一周内这种汽车销售了 $b$ 辆,那么这周的销售额为多少万元?
(4)如图所示的是某古城墙及门洞的示意图,其中门洞的下部是长方形,上部是半圆形,它的面积是多少?若城墙上面的垛口都可看作长为 $a$,宽为 $b$ 的长方形,则每个垛口的面积是多少?
 ]
]
答案:
解:
(1)x²y,是单项式,系数是1,次数是3.
(2)150-m,是多项式,次数是1.
(3)0.9ab,是单项式,系数是0.9,次数是2.
$(4)2rh+\frac{1}{2}πr²,$是多项式,次数是2;ab,是单项式,系数是1,次数是2.
(1)x²y,是单项式,系数是1,次数是3.
(2)150-m,是多项式,次数是1.
(3)0.9ab,是单项式,系数是0.9,次数是2.
$(4)2rh+\frac{1}{2}πr²,$是多项式,次数是2;ab,是单项式,系数是1,次数是2.
查看更多完整答案,请扫码查看


