《2025年名校课堂七年级数学上册北师大版江西专版》

10. 当 $a$ 是正整数时，整式 $a^{3} - 3a^{2} + 7a + 7 + (3 - 2a + 3a^{2} - a^{3})$化简后的结果一定是(C)

A.3 的整数倍
B.4 的整数倍
C.5 的整数倍
D.10 的整数倍

答案： C

11. 乐乐停车场为 24 小时营业，其收费方式如下表所示：

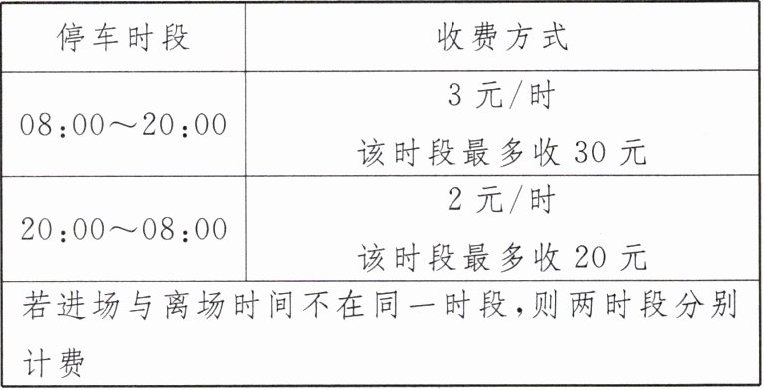
已知小李某日 $10:00$ 进场停车，停了 $x$ 小时后离场，$x$ 为整数. 若小李离场时间介于当日的 $20:00\sim24:00$ 间，则他此次停车的费用为(B)

A.$(2x + 30)$元
B.$(2x + 10)$元
C.50 元
D.$(2x - 20)$元

答案： B

12. 已知关于 $x$，$y$ 的多项式$(2x^{2} + ax - y + 6) - (2bx^{2} - 3x + 5y - 1)$的值与 $x$ 的取值无关，求 $a$，$b$ 的值.

答案： 解：原式=2x²+ax-y+6-2bx²+3x-5y+1=(2-2b)x²+(a+3)x-6y+7.
∵多项式的值与x的取值无关，
∴2-2b=0且a+3=0，解得a=-3,b=1.

13. 在学习过程中，我们要善于归纳、总结和反思. 根据所学知识，反思和解决问题：
【特例呈现】
$5 - 4 = 1＞0$；$8 - 3 = 5＞0$；$4 - 4 = 0$；$3 - 5 = -2＜0$；$10 - 15 = -5＜0$.
【知识总结】
(1) 当被减数大于减数时，差大于 0，即大减小差为正；当被减数等于减数时，差等于 0；当被减数小于减数时，差小于0，即小减大差为负. (填“大于”“小于”或“等于”)
【知识反思】
(2) 如何用上述结论比较两个有理数 $a$ 与 $b$ 的大小：当a-b＞0时，a＞b；当a-b＜0时，a＜b；当a-b=0时，a=b.
【知识应用】
(3) 运用上面反思得到的方法解答：
设 $M = x^{2} - 6x + 25$，$N = -6x + 10$，比较 $M$ 与 $N$ 的大小.

答案： 解：
(1)小于
(2)当a-b＞0时，a＞b；当a-b＜0时，a＜b；当a-b=0时，a=b
(3)M-N=(x²-6x+25)-(-6x+10)=x²-6x+25+6x-10=x²+15.
∵x²为非负数，
∴x²+15＞0，即M-N＞0.
∴M＞N.

(教材 P106 复习题 T14)在下列各式的括号内填上恰当的项：
(1)$-a + b - c + d = -a + ($b-c+d$)$.
(2)$-a + b - c + d = -($a-b+c$)+d$.
(3)$-a + b - c + d = -a + b - ($c-d$)$.
(4)$-a + b - c + d = -($a-b+c-d$)$.

答案：
(1)b-c+d
(2)a-b+c
(3)c-d
(4)a-b+c-d

1. 下列添括号正确的是(C)

A.$x + y = -(x - y)$
B.$x - y = -(x + y)$
C.$-x + y = -(x - y)$
D.$-x - y = -(x - y)$

答案： 1.C

2. 已知$2a - 3ab + 4a^{2} - 1 = 2a - ($3ab-4a²+1$)$，则括号中所填入的整式应是3ab-4a²+1.

答案： 2.3ab-4a²+1

3. 若$a + b = -1$，则$(a + b)^{2} - a - b + 5$的值是7.

答案： 3.7