第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 已知 $ a = - 3 $,则代数式 $ a ^ { 2 } + 1 $ 的值为(
A.$ - 5 $
B.$ 7 $
C.$ - 8 $
D.$ 10 $
D
)A.$ - 5 $
B.$ 7 $
C.$ - 8 $
D.$ 10 $
答案:
D
2. 若 $ a = 4 $,$ b = 10 $,则代数式 $ a ^ { 3 } - a b $ 的值为(
A.$ 14 $
B.$ 24 $
C.$ 20 $
D.$ 12 $
B
)A.$ 14 $
B.$ 24 $
C.$ 20 $
D.$ 12 $
答案:
B
3. 根据流程图中的程序,当输入 $ x $ 的值为 $ - 2 $ 时,输出的值为(

A.$ 4 $
B.$ 6 $
C.$ 8 $
D.$ 10 $
A
)
A.$ 4 $
B.$ 6 $
C.$ 8 $
D.$ 10 $
答案:
A
4. 若 $ a = - 2 $,$ b = 3 $,$ c = 4 $,则代数式 $ b ^ { 2 } - 4 a c $ 的值是
41
。
答案:
41
5. 请写出一个含 $ x $ 的代数式,且当 $ x = 4 $ 时,代数式的值为 $ - 20 $:
-5x
。
答案:
-5x
6. 若 $ a $,$ b $ 互为相反数,则代数式 $ a + b - 2 $ 的值为
-2
。
答案:
-2
7. 如图,小红要购买黑、白两种颜色的珠子串成一串手链,已知黑色珠子每颗 $ a $ 元,白色珠子每颗 $ b $ 元。
(1)小红购买这些珠子共花费
(2)当 $ a = 2 $,$ b = 3.5 $ 时,小红购买这些珠子共花费

(1)小红购买这些珠子共花费
(5a + 6b)
元。(2)当 $ a = 2 $,$ b = 3.5 $ 时,小红购买这些珠子共花费
31
元。
答案:
(1)$(5a + 6b)$
(2)31
(1)$(5a + 6b)$
(2)31
8. 人们常用公式 $ \frac { n ( a + b ) } { 2 } $ 来计算堆成如图所示形状的钢管的根数,其中 $ a $ 是顶层的根数,$ b $ 是底层的根数,$ n $ 是层数。如果一堆钢管有 $ 6 $ 层,顶层、底层的钢管数量分别为 $ 5 $ 根、$ 10 $ 根,求这堆钢管的根数。


答案:
解:$\because n = 6,a = 5,b = 10,\therefore\frac{n(a + b)}{2}=\frac{6×(5 + 10)}{2}=45$。答:这堆钢管的根数是45根。
9. 某网店进行促销,将原价为 $ a $ 元的商品以 $ ( 0.8 a - 20 ) $ 元出售,则该网店对该商品促销的方法是
打八折后再让利20元
。
答案:
打八折后再让利20元
10. (2023·无锡)当 $ a = 2 $,$ b = - 3 $ 时,代数式 $ ( a - b ) ^ { 2 } + 2 a b $ 的值为(
A.$ 13 $
B.$ 27 $
C.$ - 5 $
D.$ - 7 $
A
)A.$ 13 $
B.$ 27 $
C.$ - 5 $
D.$ - 7 $
答案:
A
11. 新考向 开放性问题 对代数式“$ 0.6 a $”可以解释为:已知一件商品的原价为 $ a $ 元,若按原价的六折出售,则这件商品现在的售价是 $ 0.6 a $ 元。请对“$ 0.6 a $”再赋予一个含义:
已知练习本每本0.6元,某人买了a本,共付款0.6a元
。
答案:
已知练习本每本0.6元,某人买了$a$本,共付款$0.6a$元
12.(1)填写下表,并观察下列两个代数式的值的变化情况
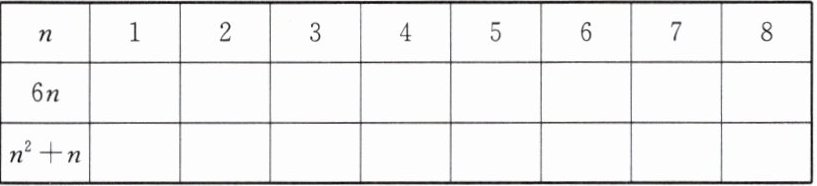
(2)随着 $ n $ 的逐渐变大,两个代数式的值如何变化?
(3)估计一下,哪个代数式的值先超过 $ 100 $。

(2)随着 $ n $ 的逐渐变大,两个代数式的值如何变化?
(3)估计一下,哪个代数式的值先超过 $ 100 $。
答案:
(1)表格填写:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|----|----|----|----|----|----|----|----|----|
| 6n | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 |
| n²+n | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 |
(2)随着n的逐渐变大,两个代数式的值都逐渐增大。
(3)对于6n:令6n>100,解得n>100/6≈16.67,n=17时6×17=102>100;
对于n²+n:n=10时,10²+10=110>100,n=9时9²+9=90<100。
故n²+n的值先超过100。
结论:
(2)两个代数式的值都逐渐增大;
(3)n²+n的值先超过100。
(1)表格填写:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|----|----|----|----|----|----|----|----|----|
| 6n | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 |
| n²+n | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 |
(2)随着n的逐渐变大,两个代数式的值都逐渐增大。
(3)对于6n:令6n>100,解得n>100/6≈16.67,n=17时6×17=102>100;
对于n²+n:n=10时,10²+10=110>100,n=9时9²+9=90<100。
故n²+n的值先超过100。
结论:
(2)两个代数式的值都逐渐增大;
(3)n²+n的值先超过100。
13. A|湖南师大附中校本经典题 如图,在一个边长为 $ b \mathrm { cm } $ 的正方形的四角各剪去一个半径为 $ a \mathrm { cm } $($ a $ 不超过 $ \frac { b } { 2 } $)的 $ \frac { 1 } { 4 } $ 圆。请用代数式表示阴影部分的面积,并求当 $ a = 2 $,$ b = 6 $ 时阴影部分的面积(结果保留 $ \pi $)。


答案:
解:由题意可得,阴影部分的面积为$(b^{2}-\pi a^{2})cm^{2}$,当$a = 2,b = 6$时,原式$=6^{2}-\pi×2^{2}=(36 - 4\pi)cm^{2}$。
查看更多完整答案,请扫码查看


