《2025年名校课堂七年级数学上册北师大版江西专版》

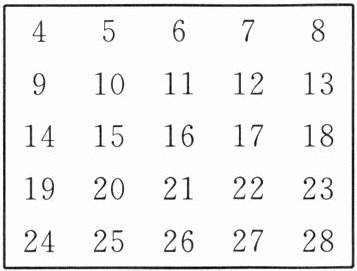
1. 下图是一个数表的一部分.
(1) 在数表中, 横行、竖列上相邻的两数之间有什么关系?
(2) 如果告诉你一竖列上连续三个数的和为 72, 你能知道是哪几个数吗?

答案： 1.解：
(1)横行上相邻两数之差(大数减去小数)为1，竖列上相邻两数之差(大数减去小数)为5。
(2)设这三个数分别为$x - 5$，$x$，$x + 5$。根据题意，得$(x - 5) + x + (x + 5) = 72$，解得$x = 24$。所以$x - 5 = 24 - 5 = 19$，$x + 5 = 24 + 5 = 29$。答：这三个数分别是19，24，29。

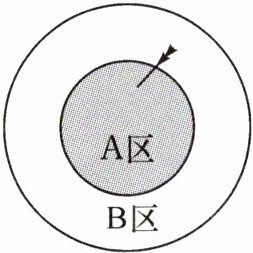
2. (2023·河北) 某磁性飞镖游戏的靶盘如图所示. 珍珍玩了两局, 每局投 10 次飞镖, 若投到边界, 则不计人次数, 需重新投. 计分规则如下:

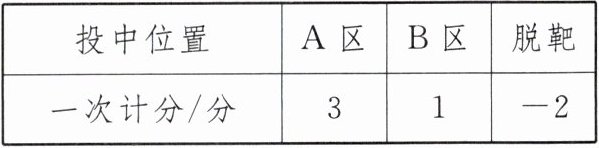
在第一局中, 珍珍投中 A 区 4 次、B 区 2 次, 脱靶 4 次.
(1) 求珍珍第一局的得分.
(2) 第二局, 珍珍投中 A 区 $ k $ 次、B 区 3 次, 其余全部脱靶. 若本局得分比第一局提高了 13 分, 求 $ k $ 的值.

答案： 2.解：
(1)由题意，得$4×3 + 2×1 + 4×(-2) = 6$(分)。答：珍珍第一局的得分为6分。
(2)由题意，得$3k + 3×1 + (10 - k - 3)×(-2) = 6 + 13$，解得$k = 6$。

3. 唐代大诗人李白喜好饮酒作诗, 民间有“李白斗酒诗百篇”之说. 《算法统宗》中记载了一个“李白沽酒”的故事. 诗云: 今携一壶酒, 游春郊外走. 逢朋加一倍, 人店饮半斗. 相逢三处店, 饮尽壶中酒. 试问能算士, 如何知原有 (注: 古代一斗是 10 升). 大意是: 李白在郊外春游时, 作出这样一条约定——遇见朋友, 到酒店里先将壶里的酒增加一倍, 再喝掉其中的 5 升酒. 按照这样的约定, 在第 3 个店里正好喝光了壶中的酒. 请问各位, 壶中原有多少升酒?

答案： 3.解：设壶中原有$x$升酒。根据题意，得$2[2(2x - 5) - 5] - 5 = 0$，解得$x = \frac {35}{8}$。答：壶中原有$\frac {35}{8}$升酒。

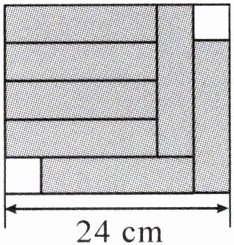
4. 如图, 用 7 个完全相同的长方形拼成了图中的阴影部分. 图中的空白部分为两个完全相同的正方形. 求图中空白部分的面积.

答案： 4.解：设7个完全相同的长方形的宽为$x$cm，则长为$4x$cm。根据题意，得$x = 24 - x - 4x$，解得$x = 4$。
∴空白部分两个正方形的边长都为4cm。
∴图中空白部分的面积为$4^{2}×2 = 32(cm^{2})$。