第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 设一个长方形的长与宽分别为 $a\ m$,$b\ m$,当该长方形的面积为 $24\ m^2$ 时,长与宽的关系可用式子表示为
ab=24
,它们成反
比例关系。
答案:
1.ab=24 反
2. 下列式子中,$y$ 与 $x$ 成反比例关系的是(
A.$y = 2x + 1$
B.$y = x^2$
C.$xy = 3$
D.$y = \frac{x}{4}$
C
)A.$y = 2x + 1$
B.$y = x^2$
C.$xy = 3$
D.$y = \frac{x}{4}$
答案:
2.C
3. 下列相关联的量成反比例关系的是 (
A.购买同一本书的总人数和总钱数
B.三角形的面积一定,则三角形的底边与该底边上的高成反比例关系
C.定期一年的利息和本金
D.一辆匀速行驶的汽车,行驶的路程与行驶的时间
B
)A.购买同一本书的总人数和总钱数
B.三角形的面积一定,则三角形的底边与该底边上的高成反比例关系
C.定期一年的利息和本金
D.一辆匀速行驶的汽车,行驶的路程与行驶的时间
答案:
3.B
4.(教材 P75 练习 T2 变式)判断下面各题中的两个量是否成反比例关系,并说明理由。
(1)圆柱的侧面积一定,圆柱的底面周长和高。
(2)打同一份稿件,打字的速度和打字所用的时间。
(3)商品的数量一定,商品的单价和总价。
(1)圆柱的侧面积一定,圆柱的底面周长和高。
(2)打同一份稿件,打字的速度和打字所用的时间。
(3)商品的数量一定,商品的单价和总价。
答案:
4.解:
(1)圆柱的底面周长和高成反比例关系.理由:
∵圆柱的底面周长和高,一个量变化,另一个量也随着变化,且这两个量的乘积(即圆柱的侧面积)一定,
∴圆柱的底面周长和高成反比例关系.
(2)打字的速度和打字所用的时间成反比例关系.理由:
∵打字的速度和打字所用的时间,一个量变化,另一个量也随着变化,且这两个量的乘积(即稿件的总字数)一定,
∴打字的速度和打字所用的时间成反比例关系.
(3)商品的单价和总价不成反比例关系.理由:商品的数量一定,商品的单价和总价成正比例关系.
(1)圆柱的底面周长和高成反比例关系.理由:
∵圆柱的底面周长和高,一个量变化,另一个量也随着变化,且这两个量的乘积(即圆柱的侧面积)一定,
∴圆柱的底面周长和高成反比例关系.
(2)打字的速度和打字所用的时间成反比例关系.理由:
∵打字的速度和打字所用的时间,一个量变化,另一个量也随着变化,且这两个量的乘积(即稿件的总字数)一定,
∴打字的速度和打字所用的时间成反比例关系.
(3)商品的单价和总价不成反比例关系.理由:商品的数量一定,商品的单价和总价成正比例关系.
5. 如下表,如果 $x$ 和 $y$ 成反比例关系,那么“■”处应填(
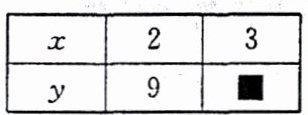
A.$3$
B.$5$
C.$6$
D.$8$
C
)
A.$3$
B.$5$
C.$6$
D.$8$
答案:
5.C
6. 新考向 跨学科 同学们在探究“杠杆原理”时,通过实验发现,当左边刻度 $4$ 上放 $3$ 个砝码,右边刻度及放砝码数如图所示时,两边平衡。想一想:在右边其余刻度上放几个砝码才能保证平衡?
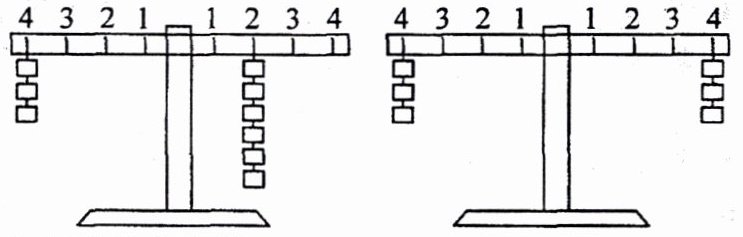
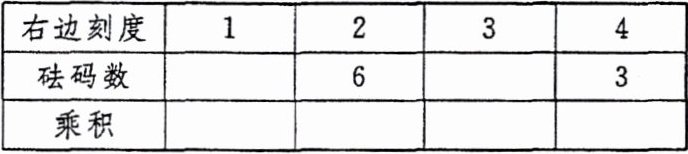
(1)请完成表格。
(2)从表中你发现刻度数和砝码数成什么比例关系?为什么?


(1)请完成表格。
(2)从表中你发现刻度数和砝码数成什么比例关系?为什么?
答案:
6.解:
(1)12 4 12 12 12 12
(2)刻度数和砝码数成反比例关系.理由:
∵刻度数和砝码数,一个量变化,另一个量也随着变化,且由表格可知,刻度数和砝码数的乘积为定值12,
∴刻度数和砝码数成反比例关系.
(1)12 4 12 12 12 12
(2)刻度数和砝码数成反比例关系.理由:
∵刻度数和砝码数,一个量变化,另一个量也随着变化,且由表格可知,刻度数和砝码数的乘积为定值12,
∴刻度数和砝码数成反比例关系.
7.(教材 P76 习题 T5 变式)食品加工厂准备把一批新酿的醋装瓶运往商店。把这批醋平均分装在若干瓶子里,每瓶的容量和所装瓶数如下表:

(1)这批新酿的醋共有多少毫升?
(2)所装瓶数是怎样随着每瓶的容量的变化而变化?
(3)用 $n$ 表示所装瓶数,$m$ 表示每瓶的容量,用式子表示 $n$ 与 $m$ 的关系。$n$ 与 $m$ 成什么比例关系?

(1)这批新酿的醋共有多少毫升?
(2)所装瓶数是怎样随着每瓶的容量的变化而变化?
(3)用 $n$ 表示所装瓶数,$m$ 表示每瓶的容量,用式子表示 $n$ 与 $m$ 的关系。$n$ 与 $m$ 成什么比例关系?
答案:
7.解:
(1)500×600=300000(mL).答:这批新酿的醋共有300000mL.
(2)所装瓶数随着每瓶的容量的变大而变小.
(3)mn=300000.n与m成反比例关系.
(1)500×600=300000(mL).答:这批新酿的醋共有300000mL.
(2)所装瓶数随着每瓶的容量的变大而变小.
(3)mn=300000.n与m成反比例关系.
查看更多完整答案,请扫码查看


