《2025年名校课堂七年级数学上册人教版》

10. 已知 a，b 是有理数，那么下列说法中，一定正确的是 (D)

A.如果 a ＜ 0，b ＜ 0，那么 a + b ＞ 0
B.如果 a ＞ 0，b ＜ 0，那么 a + b ＞ 0
C.如果 a ＞ 0，b ＜ 0，那么 a + b ＜ 0
D.如果 a ＜ 0，b ＞ 0，且 |a| ＞ |b|，那么 a + b ＜ 0

答案： 10.D

11. 如图，在数轴上，点 A，B 表示的数分别是 a，b，且 a + b = 0.若 A，B 两点的距离为 8 个单位长度，则 a 的值为 (D)


A.0
B.-8
C.4
D.-4

答案： 11.D

12. 请你设计一个实际背景来表示加法算式 (-4) + 3 的实际意义：_.早晨的气温是零下4℃，中午上升了3℃，则中午的气温是(-4)+3=-1(℃)(答案不唯一)

答案： 12.早晨的气温是零下4℃，中午上升了3℃，则中午的气温是(-4)+3=-1(℃)(答案不唯一)

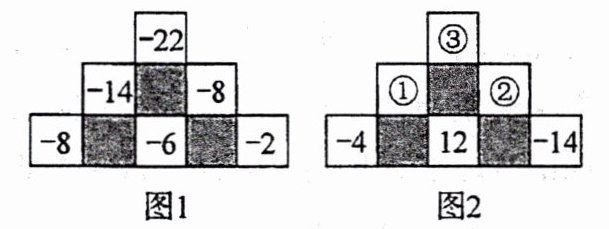
13. 石家庄外国语校本经典题 从图 1 中找规律，并按此规律，在图 2 的空格里分别填上合适的数，则①为 8，②为 -2，③为 6.

答案： 13.8 -2 6

14. 计算：
(1) (-3$\frac{2}{3}$) + 1$\frac{1}{6}$.
(2) (-2.3) + | -3.3 |.

答案： 14.解：
(1)原式$=-(3\frac{2}{3}-1\frac{1}{6})=-2\frac{1}{2}.(2)$原式=(-2.3)+3.3=+(3.3-2.3)=1.

15. 下表是某水库一周内的水位变化情况，“+”表示水位比前一天上升，“-”表示水位比前一天下降，该水库的警戒水位是 32 米，已知上周周日的水位是 30 米.

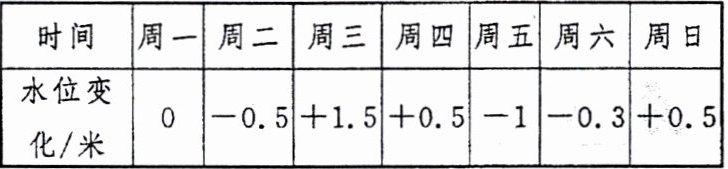
(1) 小亮认为本周内周五的水位变化值为“-1”，所以这一天的水位最低，并且最低值为 29 米；小丽认为周五的水位变化值为“-1”表示本周内周五的水位下降量最大，并不表示周五的水位最低.你认为 小丽(填“小亮”或“小丽”)的想法正确.
(2) 本周哪一天该水库的水位最高？最高水位是否达到警戒水位？

答案： 15.解：
(1)小丽
(2)周一的水位是30+0=30(米)，周二的水位是30+(-0.5)=29.5(米)，周三的水位是29.5+1.5=31(米)，周四的水位是31+0.5=31.5(米)，周五的水位是31.5+(-1)=30.5(米)，周六的水位是30.5+(-0.5)=30(米)，周日的水位是30+0.7=30.7(米).
∵29.5＜30＜30.2＜30.5＜30.5＜30.7＜31＜31.5，
∴周四的水位最高，最高水位是31.5米.31.5＜32，
∴最高水位没有达到警戒水位.

16. (1) 已知 |a| = 8，|b| = 2.
① 当 a，b 同号时，求 a + b 的值.
② 当 a，b 异号时，求 a + b 的值.
(2) 已知 |a| = 3，|b| = 1，且 a ＞ b，则 a + b 的值为 4或2.
(3) 已知 |a| = 3，|b| = 4，则 a + b = ±1或±7.

答案： 16.解：
(1)①
∵|a|=8,|b|=2，且a,b同号，
∴a=8,b=2或a=-8,b=-2.则a+b=10或-10.②
∵|a|=8,|b|=2，且a,b异号，
∴a=8,b=-2或a=-8,b=2.则a+b=6或-6.
(2)4或2
(3)±1或±7