第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 观察下列各数的排列规律:$0$,$-3$,$8$,$-15$,$\cdots$,照这样排列,第$8$个数应是(
A.$55$
B.$-56$
C.$-63$
D.$65$
C
)A.$55$
B.$-56$
C.$-63$
D.$65$
答案:
1.C
2. 新考向 数学文化 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现这样一组数:$1$,$1$,$2$,$3$,$5$,$8$,$13$,$\cdots$,根据这组数的规律,则第$10$个数是
55
.
答案:
2.55
3. 观察下列等式:$1^{3}=1^{2}$;$1^{3}+2^{3}=3^{2}$;$1^{3}+2^{3}+3^{3}=6^{2}$;$1^{3}+2^{3}+3^{3}+4^{3}=10^{2}$.根据此规律,计算$1^{3}+2^{3}+3^{3}+\cdots +7^{3}$的结果为
28²(或784)
.
答案:
3.28²(或784)
4. 观察下列等式:$3^{1}-1=2$;$3^{2}-1=8$;$3^{3}-1=26\cdots\cdots$猜测$3^{2025}-1$的个位数字是
2
.
答案:
4.2
5. 如图,刘老师把教室里的白板密码设置成了数学问题,小明同学看到图片后思索了片刻,之后输入密码,顺利地进入了白板页面,那么他输入的密码是(

A.jia362627
B.jia363672
C.jia363627
D.jia362672
B
)
A.jia362627
B.jia363672
C.jia363627
D.jia362672
答案:
5.B
6. 观察下列图形中的数字排列规律,在第⑧个图中,$b - c$的值是(

A.$-382$
B.$-386$
C.$126$
D.$382$
D
)
A.$-382$
B.$-386$
C.$126$
D.$382$
答案:
6.D
7. 观察以下等式:
第$1$个等式:$\frac{1}{1}+\frac{0}{2}+\frac{1}{1}×\frac{0}{2}=1$;
第$2$个等式:$\frac{1}{2}+\frac{1}{3}+\frac{1}{2}×\frac{1}{3}=1$;
第$3$个等式:$\frac{1}{3}+\frac{2}{4}+\frac{1}{3}×\frac{2}{4}=1$;
第$4$个等式:$\frac{1}{4}+\frac{3}{5}+\frac{1}{4}×\frac{3}{5}=1$;
第$5$个等式:$\frac{1}{5}+\frac{4}{6}+\frac{1}{5}×\frac{4}{6}=1$;
$\cdots\cdots$
按照以上规律,解决下列问题:
(1)写出第$6$个等式:
(2)利用规律简便运算:$\frac{1}{6}+\frac{1}{8}+\frac{5}{7}+\frac{7}{9}+\frac{5}{42}+\frac{7}{72}$.
第$1$个等式:$\frac{1}{1}+\frac{0}{2}+\frac{1}{1}×\frac{0}{2}=1$;
第$2$个等式:$\frac{1}{2}+\frac{1}{3}+\frac{1}{2}×\frac{1}{3}=1$;
第$3$个等式:$\frac{1}{3}+\frac{2}{4}+\frac{1}{3}×\frac{2}{4}=1$;
第$4$个等式:$\frac{1}{4}+\frac{3}{5}+\frac{1}{4}×\frac{3}{5}=1$;
第$5$个等式:$\frac{1}{5}+\frac{4}{6}+\frac{1}{5}×\frac{4}{6}=1$;
$\cdots\cdots$
按照以上规律,解决下列问题:
(1)写出第$6$个等式:
$\frac{1}{6}+\frac{5}{7}+\frac{1}{6}×\frac{5}{7}=1$
.(2)利用规律简便运算:$\frac{1}{6}+\frac{1}{8}+\frac{5}{7}+\frac{7}{9}+\frac{5}{42}+\frac{7}{72}$.
答案:
7.解:
(1)$\frac{1}{6}+\frac{5}{7}+\frac{1}{6}×\frac{5}{7}=1$
(2)原式=($\frac{1}{6}+\frac{5}{7}+\frac{1}{6}×\frac{5}{7}$)+($\frac{1}{8}+\frac{7}{9}+\frac{1}{8}×\frac{7}{9}$)=1+1=2。
(1)$\frac{1}{6}+\frac{5}{7}+\frac{1}{6}×\frac{5}{7}=1$
(2)原式=($\frac{1}{6}+\frac{5}{7}+\frac{1}{6}×\frac{5}{7}$)+($\frac{1}{8}+\frac{7}{9}+\frac{1}{8}×\frac{7}{9}$)=1+1=2。
8. 观察下面一组数:$-1$,$2$,$-3$,$4$,$-5$,$6$,$-7$,$\cdots$,将这组数按照下图中的规律排下去.
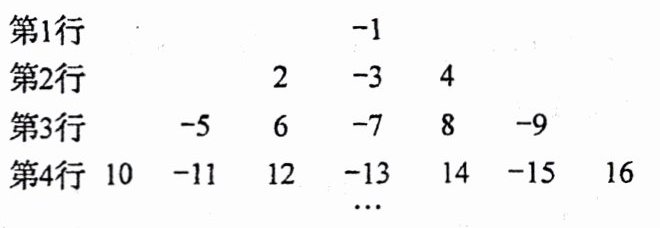
(1)第$10$行从左往右第$4$个数是
(2)求前$7$行的数字总和.
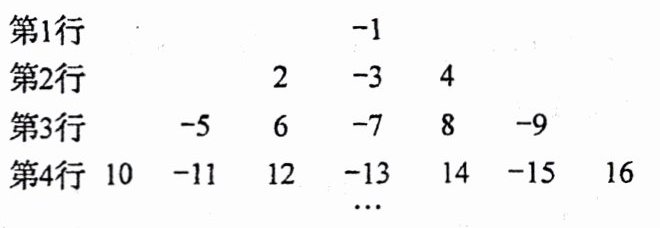
(1)第$10$行从左往右第$4$个数是
-85
.(2)求前$7$行的数字总和.
答案:
8.解:
(1)-85
(2)由规律可知,第7行最后一个数为-49,
∴前7行的数字总和为-1+2-3+4-5+6-7+8-9+10-…-47+48-49=(-1+2)+(-3+4)+…+(-47+48)-49=24-49=-25。
(1)-85
(2)由规律可知,第7行最后一个数为-49,
∴前7行的数字总和为-1+2-3+4-5+6-7+8-9+10-…-47+48-49=(-1+2)+(-3+4)+…+(-47+48)-49=24-49=-25。
查看更多完整答案,请扫码查看


