第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
数学活动 1 整理家庭收支账目
下表是小明家 2024 年 12 个月的收支账目(不完整),小明将家庭支出费用(单位:元)分为三部分,一是基本生活费,包括水电费、通信费、交通费、餐饮费、物业费、取暖费等;二是临时性费用,包括节日采购、礼金、旅游等;三是子女教育费。将收人记为正数,支出记为负数,请根据表格信息完成下列任务。
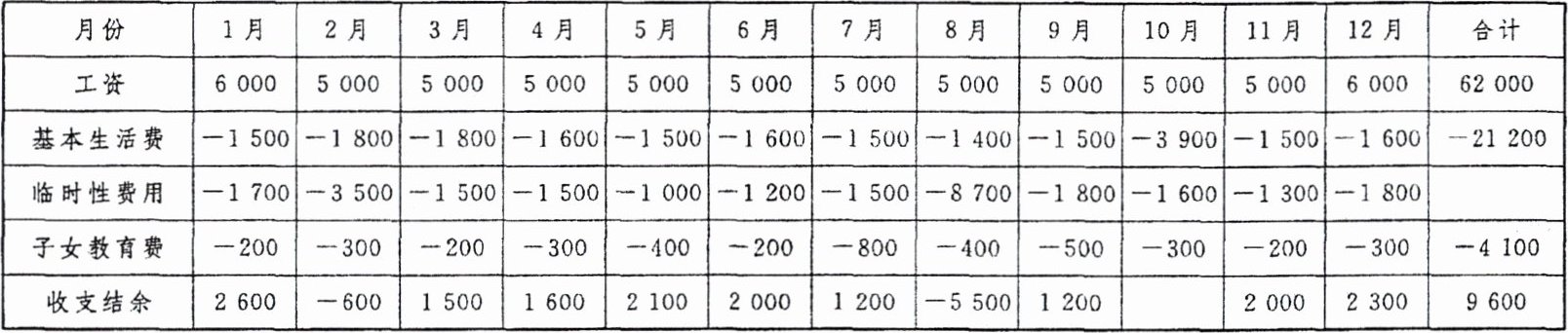
(1)计算 10 月份收支结余及 2024 年全年临时性费用,并将结果直接填人上表的空格处。
(2)根据以上信息,请给小明家今后家庭理财提出合理化的建议。
下表是小明家 2024 年 12 个月的收支账目(不完整),小明将家庭支出费用(单位:元)分为三部分,一是基本生活费,包括水电费、通信费、交通费、餐饮费、物业费、取暖费等;二是临时性费用,包括节日采购、礼金、旅游等;三是子女教育费。将收人记为正数,支出记为负数,请根据表格信息完成下列任务。

(1)计算 10 月份收支结余及 2024 年全年临时性费用,并将结果直接填人上表的空格处。
(2)根据以上信息,请给小明家今后家庭理财提出合理化的建议。
答案:
(1)-27 100 -800
(2)小明家临时性费用开支较大,子女教育费用相对较小,今后应减少临时性开支,例如:适当减少节日采购、礼金、旅游等费用,养成节约的好习惯,适当加大子女教育费用.(答案不唯一)
(1)-27 100 -800
(2)小明家临时性费用开支较大,子女教育费用相对较小,今后应减少临时性开支,例如:适当减少节日采购、礼金、旅游等费用,养成节约的好习惯,适当加大子女教育费用.(答案不唯一)
综合与实践
【主题】探索神奇的幻方.
【阅读】幻方的历史悠久,传说最早出现在夏禹时代的“洛书”(如图 1)。“洛书”是一种关于天地空间变化脉络的图案,它以黑点与白点为基本要素,以一定方式构成若干个不同的组合。“洛书”用今天的数学符号翻译出来就是一个三阶幻方(如图 2),三阶幻方又名九宫格,是一种将数字 1~9(数字不重复使用)安排在三行三列的正方形格子中,使每行、每列和每条对角线上的数字之和都相等。
【实践】
(1)根据“洛书”中表达的意思,将图 2 中的三阶幻方补充完整。
【提升】
(2)改变图 2 幻方中数字的位置,可以得到一个新的三阶幻方(如图 3),且每行、每列和每条对角线上的数字之和仍都相等,请补全这个新的三阶幻方。
【拓展】
(3)图 4 有 3 个正方形,每个正方形的顶点处都有一个“○”。将-11,-9,-7,-5,-3,-1,2,4,6,8,10,12 这 12 个数填入恰当的位置(数字不重复使用),使每个正方形的 4 个顶点“○”中的数字之和都为 2,并求出 $ mn $ 的值。

【主题】探索神奇的幻方.
【阅读】幻方的历史悠久,传说最早出现在夏禹时代的“洛书”(如图 1)。“洛书”是一种关于天地空间变化脉络的图案,它以黑点与白点为基本要素,以一定方式构成若干个不同的组合。“洛书”用今天的数学符号翻译出来就是一个三阶幻方(如图 2),三阶幻方又名九宫格,是一种将数字 1~9(数字不重复使用)安排在三行三列的正方形格子中,使每行、每列和每条对角线上的数字之和都相等。
【实践】
(1)根据“洛书”中表达的意思,将图 2 中的三阶幻方补充完整。
【提升】
(2)改变图 2 幻方中数字的位置,可以得到一个新的三阶幻方(如图 3),且每行、每列和每条对角线上的数字之和仍都相等,请补全这个新的三阶幻方。
【拓展】
(3)图 4 有 3 个正方形,每个正方形的顶点处都有一个“○”。将-11,-9,-7,-5,-3,-1,2,4,6,8,10,12 这 12 个数填入恰当的位置(数字不重复使用),使每个正方形的 4 个顶点“○”中的数字之和都为 2,并求出 $ mn $ 的值。

答案:
(1)9 3
(2) 6 5 4
(3) 正方形的4个顶点“$○$”中的数字之和都为2,$\therefore m = 2 - (4 + 2 - 3) = -1,k = 2 - (8 - 7 - 5) = 6$.$\because$填人的数字不重复,$\therefore l = - 11,n = 10$或$l = 10,n = - 11.\therefore mn = - 1 × 10 = - 10$或$mn = -1 × ( - 11) = 11$.
(1)9 3
(2) 6 5 4
(3) 正方形的4个顶点“$○$”中的数字之和都为2,$\therefore m = 2 - (4 + 2 - 3) = -1,k = 2 - (8 - 7 - 5) = 6$.$\because$填人的数字不重复,$\therefore l = - 11,n = 10$或$l = 10,n = - 11.\therefore mn = - 1 × 10 = - 10$或$mn = -1 × ( - 11) = 11$.
查看更多完整答案,请扫码查看


