第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 下列式子中,是方程的是(
A.$25x$
B.$15 - 3 = 12$
C.$6x + 1 = 6$
D.$4x + 7 < 9$
C
)A.$25x$
B.$15 - 3 = 12$
C.$6x + 1 = 6$
D.$4x + 7 < 9$
答案:
1.C
2. 根据题意列方程.
(1)$x$的5倍比$x$的2倍小12:
(2)$x$的$\frac{1}{7}$与3的差等于最大的一位数:
(1)$x$的5倍比$x$的2倍小12:
2x-5x=12
.(2)$x$的$\frac{1}{7}$与3的差等于最大的一位数:
\frac{1}{7}x - 3=9
.
答案:
$2.(1)2x-5x=12 (2)\frac{1}{7}x - 3=9$
3. 【原创】根据下列图形中标出的量及其满足的关系,列出方程:
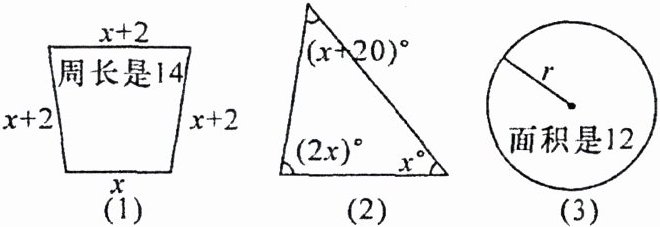
(1)
(2)
(3)

(1)
x+(x + 2)+(x + 2)+(x + 2)=14
.(2)
x+2x+(x + 20)=180
.(3)
$\pi r^{2}=12$
.
答案:
$3.(1)x+(x + 2)+(x + 2)+(x + 2)=14 (2)x+2x+(x + 20)=180 (3)\pi r^{2}=12$
4. (教材P113例1变式)根据下列问题,设未知数并列出方程.
(1)公园里有一个边长为6m的正方形花坛,现在想扩大花坛的面积.要使花坛的面积增加$28m^{2}$后仍然是正方形,则边长扩大多少米?
(2)某校的学生中,女生占49%,男生有1020名,则该校共有多少名学生?
(1)公园里有一个边长为6m的正方形花坛,现在想扩大花坛的面积.要使花坛的面积增加$28m^{2}$后仍然是正方形,则边长扩大多少米?
(2)某校的学生中,女生占49%,男生有1020名,则该校共有多少名学生?
答案:
4.解:
(1)设边长扩大x米,则扩大后的正方形花坛的边长为(x + 6)米,列方程为$(x + 6)^{2}=6^{2}+28。$
(2)设该校的学生数为x,则女生数为0.49x或男生数为(1 - 0.49)x,列方程为0.49x+1020=x或(1 - 0.49)x=1020。
(1)设边长扩大x米,则扩大后的正方形花坛的边长为(x + 6)米,列方程为$(x + 6)^{2}=6^{2}+28。$
(2)设该校的学生数为x,则女生数为0.49x或男生数为(1 - 0.49)x,列方程为0.49x+1020=x或(1 - 0.49)x=1020。
5. 下列式子:①$3 - 4 = -1$;②$2x - 5y$;③$x + 4 > 7$;④$1 + 2x = 0$;⑤$6x + 4y = 2$;⑥$\frac{1}{x} + 2 = y$;⑦$3x^{2} - 2x - 1 = 0$.其中是等式的是
①④⑤⑥⑦
,是方程的是④⑤⑥⑦
.(填序号)
答案:
5.①④⑤⑥⑦ ④⑤⑥⑦
6. 根据题意列出方程(不必求解).
(1)某班原分成两个小组进行课外体育活动,第一组26人,第二组22人.根据学校活动器材的数量,要将第一组的人数调整为第二组的一半,应从第一组调多少人到第二组去?
(2)小明去商店买练习本,回来后问同学:“店主告诉我,如果多买一些就给我八折优惠,我就买了20本,结果便宜了4.8元.你猜原来每本练习本的价格是多少?”
(1)某班原分成两个小组进行课外体育活动,第一组26人,第二组22人.根据学校活动器材的数量,要将第一组的人数调整为第二组的一半,应从第一组调多少人到第二组去?
(2)小明去商店买练习本,回来后问同学:“店主告诉我,如果多买一些就给我八折优惠,我就买了20本,结果便宜了4.8元.你猜原来每本练习本的价格是多少?”
答案:
6.解:
(1)设应从第一组调x人到第二组去.依题意,得$26 - x=\frac{1}{2}(22 + x)。$
(2)设原来每本练习本的价格是y元.依题意,得20y - 20y×80% = 4.8。
(1)设应从第一组调x人到第二组去.依题意,得$26 - x=\frac{1}{2}(22 + x)。$
(2)设原来每本练习本的价格是y元.依题意,得20y - 20y×80% = 4.8。
7. 根据下列问题,列方程:
(1)小明参加了一场3200米的跑步比赛,他以6米/秒的速度跑了一段路程后,又以5米/秒的速度跑完了剩下的路程,一共花了10分钟,求小明以6米/秒的速度跑了多少米.
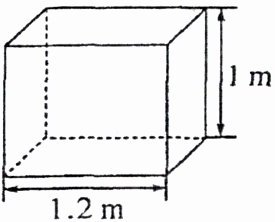
(2)如图,这是一个长方体包装盒的示意图,它的长为1.2m,高为1m,表面积为$6.8m^{2}$,则这个包装盒底面的宽为多少米?
(1)小明参加了一场3200米的跑步比赛,他以6米/秒的速度跑了一段路程后,又以5米/秒的速度跑完了剩下的路程,一共花了10分钟,求小明以6米/秒的速度跑了多少米.
(2)如图,这是一个长方体包装盒的示意图,它的长为1.2m,高为1m,表面积为$6.8m^{2}$,则这个包装盒底面的宽为多少米?

答案:
7.解:
(1)设小明以6米/秒的速度跑了x米.根据“跑x米所用的时间+跑余下路程所用的时间=10×60”,得$\frac{x}{6}+\frac{3200 - x}{5}=60×10$或$(10×60 - \frac{x}{6})+x=3200。$
(2)设包装盒底面的宽为y米.根据表面积公式,得2(1.2y+y + 1.2)=6.8。
(1)设小明以6米/秒的速度跑了x米.根据“跑x米所用的时间+跑余下路程所用的时间=10×60”,得$\frac{x}{6}+\frac{3200 - x}{5}=60×10$或$(10×60 - \frac{x}{6})+x=3200。$
(2)设包装盒底面的宽为y米.根据表面积公式,得2(1.2y+y + 1.2)=6.8。
查看更多完整答案,请扫码查看


