《2025年名校课堂七年级数学上册人教版》

【例 1】如图，点 $ C $ 在线段 $ AB $ 上，$ M $，$ N $ 分别是 $ AC $，$ BC $ 的中点。

(1)若 $ AC = 9\ cm $，$ CB = 6\ cm $，则线段 $ MN $ 的长为_______$cm$。
(2)若 $ AC = a $，$ CB = b $，则线段 $ MN $ 的长为_______。
(3)若 $ C $ 为线段 $ AB $ 上的任意一点，且 $ AB = n $，其他条件不变，你能猜想 $ MN $ 的长度吗？请用一句简洁的话描述你发现的结论。
【拓展提问】若将题干中的“点 $ C $ 在线段 $ AB $ 上”改为“点 $ C $ 在线段 $ AB $ 的延长线上”，其他条件不变，则(3)中的结论还成立吗？请画出图形，写出结论，并说明理由。

答案： 解：
(1)\frac{15}{2}
(2)\frac{a+b}{2}
(3)猜想：$MN = \frac{1}{2}AB = \frac{1}{2}n$. 结论：若C
![img alt=图片编号或题号(图片的具体编号或者所属题目的题号未明确给出，按描述为相关线段图)]
为线段AB上的任意一点，且M，N分别是AC，BC的中点，则$MN = \frac{1}{2}AB$.
【拓展提问】$MN = \frac{1}{2}n$成立. 理由如下：如图，当点C在线段AB的延长线上时，
$\because$M，N分别是AC，BC的中点，$\therefore MC = \frac{1}{2}AC$，$NC = \frac{1}{2}BC$. 又$\because MN = MC - NC$，$\therefore MN = \frac{1}{2}(AC - BC) = \frac{1}{2}AB = \frac{1}{2}n$.

1. 如图，线段 $ AB $ 的长为 $ 6 $，$ C $ 是 $ AB $ 的中点，$ D $ 是 $ BC $ 的中点，$ E $ 是 $ AD $ 的中点，求线段 $ AE $ 的长。

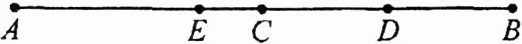
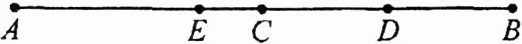
答案： 1. 解：$\because$C是AB的中点，$AC = BC = \frac{1}{2}AB = 3$. 又$\because$D是BC的中点，$\therefore BD = CD = \frac{1}{2}BC = 1.5$. $\therefore AD = AB - BD = 6 - 1.5 = 4.5$. $\because$E是AD的中点，$\therefore AE = \frac{1}{2}AD = 2.25$.

2. (1)如图，已知点 $ C $ 在线段 $ AB $ 上，且 $ AB = 20\ cm $，$ BC = 8\ cm $，$ M $，$ N $ 分别是 $ AB $，$ BC $ 的中点，求线段 $ MN $ 的长。

解：$\because AB = 20\ cm$，$ M $ 是AB的中点，
$\therefore BM = $\frac{1}{2}$ AB = 10\ cm $。
$\because BC = 8\ cm$，$ N $ 是 $ BC $ 的中点，
$\therefore BN = $\frac{1}{2}$ BC = 4\ cm $。
$\therefore MN = BM - $BN$ = 6\ cm $。
(2)若 $ C $ 是线段 $ AB $ 上任意一点，且 $ AB = a\ cm $，$ BC = b\ cm $，$ M $，$ N $ 分别是 $ AB $，$ BC $ 的中点，求线段 $ MN $ 的长。(用含 $ a $，$ b $ 的代数式表示)

答案： 2. 解：
(1)$AB = \frac{1}{2} + \frac{1}{2}BN$
(2)$\because AB = a cm$，M是AB的中点，$\therefore BM = \frac{1}{2}AB = \frac{1}{2}a cm$. $\because BC = b$，N是BC的中点，$\therefore BN = \frac{1}{2}BC = \frac{1}{2}b cm$.
$\therefore MN = BM - BN = \frac{1}{2}a - \frac{1}{2}b = \frac{a - b}{2} cm$.