第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
【知识回顾】通过对“进位制的认识与探究”的学习我们知道,进位制是人们为了记数和运算方便而约定的记数系统。在日常生活中,我们最熟悉、最常用的是十进制,十进制逢十进一,基数是 10,使用 0~9 十个数字记数;计算机常用的记数形式是二进制,二进制逢二进一,基数是 2,使用 0 和 1 两个数字记数。一个数可以表示成各数位上的数字与基数的幂的乘积之和的形式,二进制数和十进制数之间可以相互转换。(规定:$2^{0}=1$)
例:$(11)_{2}=1×2^{1}+1×2^{0}=3$;
$18=1×2^{4}+0×2^{3}+0×2^{2}+1×2^{1}+0×2^{0}=(10010)_{2}$.
任务一:
(1)将$(101)_{2}$转换成十进制数的结果为
【类比探究】二进制加法运算的基本原理与十进制相同,不同的是十进制逢十进一,二进制逢二进一.
例:$(111)_{2}+(10)_{2}=(1001)_{2}$.
任务二:
(2)①计算:$(10101)_{2}+(110)_{2}$.
②将①中结果转化为十进制数.
【迁移运用】
(3)无论是十进制、二进制、八进制还是十六进制,每种进制都有其独特的优势和应用场景.在给网页添加颜色时用到的十六进制颜色码是通过以“#”开头的六位十六进制数值来表示颜色的方法,颜色的明暗可以通过十六进制数值的大小来表示.已知将十六进制数转换成十进制数的算法与二进制数的算法类似,且十六进制数与十进制数之间的对应关系如下表:

请根据上表信息直接写出蓝色的代码$(\#0000FF)_{16}$转换为十进制数的结果.
【拓展应用】
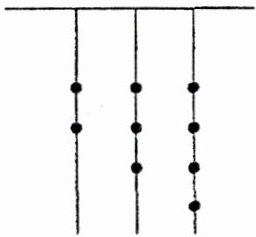
(4)《易经》中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位女孩在从右到左依次排列的绳子上打结,用来记录自己采集到的野果数,图中表示女孩用绳结记录的数字,按照六进制记数法,即右边的绳子打结满 6 个,则此绳子左边的绳子打 1 个结,原来绳子的结全部打开清零,依次类推,最左边绳子上的每个结都是中间绳子满 6 进 1 得来的.根据图中女孩所打的绳结,写出这个六进制数为(
例:$(11)_{2}=1×2^{1}+1×2^{0}=3$;
$18=1×2^{4}+0×2^{3}+0×2^{2}+1×2^{1}+0×2^{0}=(10010)_{2}$.
任务一:
(1)将$(101)_{2}$转换成十进制数的结果为
5
,将 35 转换成二进制数的结果为(100011)₂
.【类比探究】二进制加法运算的基本原理与十进制相同,不同的是十进制逢十进一,二进制逢二进一.
例:$(111)_{2}+(10)_{2}=(1001)_{2}$.
任务二:
(2)①计算:$(10101)_{2}+(110)_{2}$.
②将①中结果转化为十进制数.
【迁移运用】
(3)无论是十进制、二进制、八进制还是十六进制,每种进制都有其独特的优势和应用场景.在给网页添加颜色时用到的十六进制颜色码是通过以“#”开头的六位十六进制数值来表示颜色的方法,颜色的明暗可以通过十六进制数值的大小来表示.已知将十六进制数转换成十进制数的算法与二进制数的算法类似,且十六进制数与十进制数之间的对应关系如下表:

请根据上表信息直接写出蓝色的代码$(\#0000FF)_{16}$转换为十进制数的结果.
【拓展应用】
(4)《易经》中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位女孩在从右到左依次排列的绳子上打结,用来记录自己采集到的野果数,图中表示女孩用绳结记录的数字,按照六进制记数法,即右边的绳子打结满 6 个,则此绳子左边的绳子打 1 个结,原来绳子的结全部打开清零,依次类推,最左边绳子上的每个结都是中间绳子满 6 进 1 得来的.根据图中女孩所打的绳结,写出这个六进制数为(
234
$)_{6};$若用十进制数表示女孩采集到的野果数,则她一共采集到的野果数量为94
个.
答案:
(1)5
(100011)₂
(2)①结合例题,二进制逢二进一可得,
(10101)₂+
(110)₂=
(11011)₂,②
(11011)₂=1×2⁴+1×2³+0×2²+1×2¹+1×2⁰=27+23
(3)依题意,(#0000FF)₁₆=0×16³+0×16²+0×16¹+15×16⁰=15×16=240+15=255
(4)234 94
(1)5
(100011)₂
(2)①结合例题,二进制逢二进一可得,
(10101)₂+
(110)₂=
(11011)₂,②
(11011)₂=1×2⁴+1×2³+0×2²+1×2¹+1×2⁰=27+23
(3)依题意,(#0000FF)₁₆=0×16³+0×16²+0×16¹+15×16⁰=15×16=240+15=255
(4)234 94
查看更多完整答案,请扫码查看


