《2025年课堂精练九年级物理全一册北师大版》

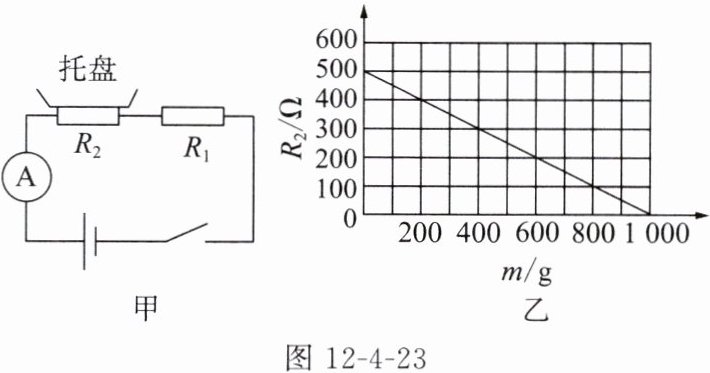
13. 图 12 - 4 - 23 甲是某科技小组制作的电子秤的原理示意图,$ R_1 $ 为定值电阻；托盘下方的电阻 $ R_2 $ 为力敏电阻,其电阻大小与托盘内所放物体的质量 $ m $ 的关系如图 12 - 4 - 23 乙所示。已知电源电压为 $ 6 \, V $。
(1)当托盘中不放任何物体时,$ R_2 $ 的阻值为500 Ω。
(2)闭合开关,若托盘中不放任何物体时,电流表的示数 $ I_1 = 0.01 \, A $,求定值电阻 $ R_1 $ 的阻值。
(3)若在托盘中放入某物体后,电流表的示数 $ I_2 = 0.02 \, A $,求该物体的质量大小。

答案： 1. （1）
由图乙可知，当托盘中不放任何物体（$m = 0$）时，$R_2$的阻值为$500\Omega$。
2. （2）
解：当托盘中不放任何物体时，$R_1$与$R_2$串联，根据欧姆定律$I=\frac{U}{R}$，此时电路中的总电阻$R=\frac{U}{I_1}$，已知$U = 6V$，$I_1 = 0.01A$，则$R=\frac{6V}{0.01A}=600\Omega$。
因为串联电路中总电阻$R = R_1+R_2$，$R_2 = 500\Omega$，所以$R_1=R - R_2$，即$R_1=600\Omega - 500\Omega = 100\Omega$。
3. （3）
解：当电流$I_2 = 0.02A$时，根据欧姆定律$R'=\frac{U}{I_2}$，$U = 6V$，$I_2 = 0.02A$，则$R'=\frac{6V}{0.02A}=300\Omega$。
因为$R' = R_1+R_2'$，$R_1 = 100\Omega$，所以$R_2'=R' - R_1$，$R_2'=300\Omega - 100\Omega = 200\Omega$。
由图乙可知，当$R_2' = 200\Omega$时，物体质量$m = 600g$。
综上，答案依次为：（1）$500\Omega$；（2）$100\Omega$；（3）$600g$。

1. 实验原理：$R=\frac{U}{I}$。

答案： $R=\frac{U}{I}$

2. 实验器材：电源、导线、开关、被测电阻、电压表、电流表、滑动变阻器等。

答案： 电压表　电流表　滑动变阻器

4. (1)在“测量定值电阻的阻值”实验中,滑动变阻器的作用是：①保护电路；②改变电阻两端的电压，进行多次测量，计算电阻并取平均值从而减小实验误差。
(2)在“测量小灯泡的电阻”实验中,发现电压表、电流表的示数变化时,灯泡的电阻也明显变化,其原因是灯泡的电阻受到温度的影响。

答案：
(1)①保护电路　②改变电阻两端的电压，进行多次测量，计算电阻并取平均值从而减小实验误差
(2)灯泡的电阻受到温度的影响

1. 在“伏安法测电阻”实验中,某同学连接了如图12-5-2所示的电路(电路元件完好,接线柱接线牢固)。

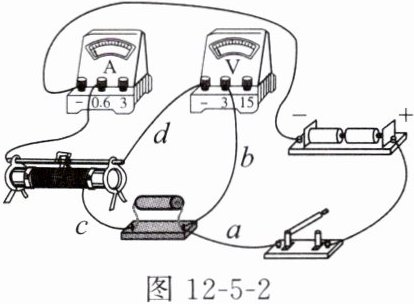
(1)在未检查电路连接是否正确的情况下,闭合开关,调节滑动变阻器的滑动头,电流表的示数将发生变化,电压表的示数将保持不变。(均选填“发生变化”或“保持不变”)
(2)检查电路,发现有一处导线连接错误,连接错误的导线是d(选填“a”“b”“c”或“d”)。
(3)纠正错误后,闭合开关,测得的几组数据如下表所示。第3次实验时电流表的示数如图12-5-3所示,为0.18A。由实验可得待测电阻的阻值为15.2(结果保留一位小数)Ω。


(4)某次实验中,闭合开关后,电流表无示数,电压表示数接近电源电压,出现这种故障的原因可能是待测电阻处发生断路。

答案：
(1)发生变化　保持不变
(2)d
(3)0.18　15.2
(4)待测电阻处发生断路