1. 如图,已知菱形$ABCD的周长为12$,$\angle A = 60^{\circ}$,则$BD$的长为(
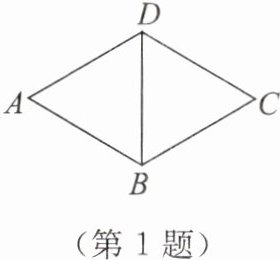
A.$3$
B.$4$
C.$6$
D.$8$
A
)。
A.$3$
B.$4$
C.$6$
D.$8$
答案:
A
2. 菱形的对角线不具有的性质是(
A.对角线互相垂直
B.对角线所在直线是对称轴
C.对角线相等
D.对角线互相平分
C
)。A.对角线互相垂直
B.对角线所在直线是对称轴
C.对角线相等
D.对角线互相平分
答案:
C
3. 在菱形$ABCD$中,$\angle A:\angle B = 1:5$,高是$8\mathrm{cm}$,则菱形的周长是
64 cm
。
答案:
64 cm
4. 菱形$OACB$在平面直角坐标系中的位置如图所示,点$C的坐标是(6,0)$,点$A的纵坐标是1$,则点$B$的坐标是
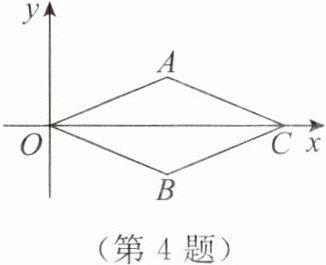
(3,-1)
。
答案:
(3,-1)
5. 已知菱形的一条对角线长为$6\mathrm{cm}$,面积为$24\mathrm{cm}^{2}$,则菱形的周长为
20 cm
。
答案:
20 cm
6. 如图,在菱形$ABCD$中,过点$B作BE\perp AD于E$,$BF\perp CD于F$,求证:$AE = CF$。
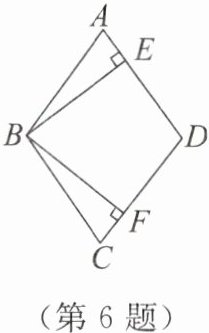

答案:
提示:根据菱形的性质和全等三角形的判定和性质证明即可.
7. 如图,在菱形$ABCD$中,$AE\perp BC于点E$,且$BE = CE$,$AD = 4$。
(1) 求$BD$的长;
(2) 求菱形$ABCD$的面积。
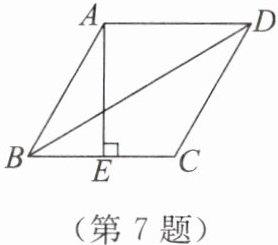
(1) 求$BD$的长;
(2) 求菱形$ABCD$的面积。

答案:
(1)$4\sqrt{3}$.
(2)$8\sqrt{3}$.
(1)$4\sqrt{3}$.
(2)$8\sqrt{3}$.
8. 如图①,菱形$ABCD的边长为2$,点$E是AB$的中点,且$DE\perp AB$。
(1) 求证:$\triangle ABD$是等边三角形;
(2) 将图①中$\triangle ADE绕点D$逆时针旋转,使得点$A和点C$重合,得到$\triangle CDF$,连接$BF$,如图②,求线段$BF$的长。
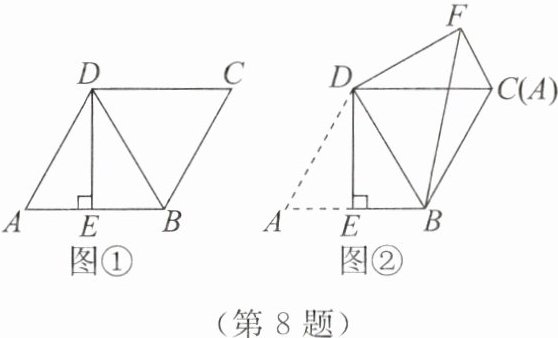
(1) 求证:$\triangle ABD$是等边三角形;
(2) 将图①中$\triangle ADE绕点D$逆时针旋转,使得点$A和点C$重合,得到$\triangle CDF$,连接$BF$,如图②,求线段$BF$的长。

答案:
提示:
(1)证明△ABD的三条边相等即可.
(2)证明∠BDF=90°,由勾股定理得BF=$\sqrt{7}$.
(1)证明△ABD的三条边相等即可.
(2)证明∠BDF=90°,由勾股定理得BF=$\sqrt{7}$.
查看更多完整答案,请扫码查看


