《2025年点金训练精讲巧练高中物理必修第一册教科版》

$7.$如图甲所示，$A$车原来临时停在一水平路面上，$B$车在后面匀速向$A$车靠近，$A$车司机发现后启动$A$车，以$A$车司机发现$B$车为计时起点($t = 0$)，$A$、$B$两车的$v-t$图像如图乙所示。已知$B$车在第$1\ s$内与$A$车的距离缩短了$x_1 = 12\ m$。

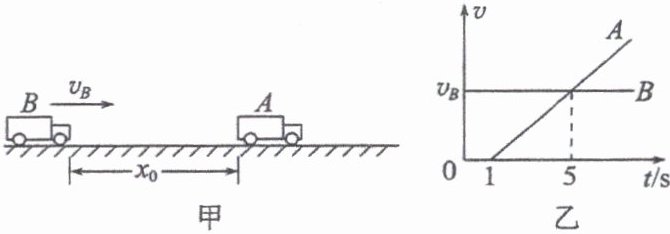
$(1)$求$B$车运动的速度$v_B$和$A$车的加速度$a$的大小。
$(2)$若$A$、$B$两车不会相撞，则$A$车司机发现$B$车时($t = 0$)两车的距离$x_0$应满足什么条件？

答案： 7.解析：
(1)在$t_{1}=1s$时A车刚启动，两车缩短的距离$x_{1}=v_{B}t_{1}$，
代入数据解得B车的速度$v_{B}=12m/s$，
A车的加速度$a=\frac{v_{B}}{t_{2}-t_{1}}$，
代入数据解得A车的加速度大小$a=3m/s^{2}$。
(2)两车的速度相等时，两车的距离达到最小值，对应于$v-t$图像的$t_{2}=5s$时刻，此时两车已发生的相对位移为图乙中梯形部分的面积，则
$x=\frac{1}{2}v_{B}(t_{1}+t_{2})$，
解得$x=36m$，
因此，若A、B两车不会相撞，则两车的距离$x_{0}$应满足条件$x_{0}＞36m$。
答案：
(1)$12m/s3m/s^{2}$
(2)$x_{0}＞36m$

$8.$中国细犬(简称细犬)是中国古老的狩猎犬种，主要分布在山东省内。某次狩猎细犬发现正南方$L = 24\ m$处有一只野兔，野兔也发现细犬并立刻向正南方逃跑，同时细犬向正南方沿直线追击野兔。已知细犬的加速度为$a_1 = 4\ m/s^2$，最大速度为$v_1 = 16\ m/s$；野兔的加速度为$a_2 = 8\ m/s^2$，最大速度为$v_2 = 8\ m/s$。
$(1)$求细犬和野兔之间的最大距离；
$(2)$经多长时间，细犬捕获野兔？
$(3)$若野兔发现细犬后，向正东方逃跑，细犬迅速判断(不计判断时间)并沿某方向直线追击拦截野兔，将其捕获，求经多长时间，细犬捕获野兔。

答案： 8.解析：
(1)野兔的最大速度为$v_{2}=8m/s$，
加速到最大速度的时间$t_{0}=\frac{v_{2}}{a_{2}}=1s$，
加速到最大速度的位移$x_{0}=\frac{v_{2}^{2}}{2a_{2}}=4m$，
当细犬的速度和野兔速度相等时两者间的距离最大，则
经过的时间$t_{1}=\frac{v_{2}}{a_{1}}=2s$，
此时细犬和野兔之间的最大距离
$x_{m}=L+x_{0}+v_{2}(t_{1}-t_{0})-\frac{1}{2}a_{1}t_{1}^{2}=28m$。
(2)细犬加速到最大速度的时间$t_{0}'=\frac{v_{1}}{a_{1}}=4s$，
加速到最大速度的位移$x_{0}'=\frac{v_{1}^{2}}{2a_{1}}=32m$，
假设细犬在加速阶段追上兔子，且经过的时间为$t$，则
$\frac{1}{2}a_{1}t^{2}=L+x_{0}+v_{2}(t-t_{0})$，
解得$t=5.7s＞4s$(另一值舍掉)，假设错误，
若细犬将在匀速阶段追上兔子，则
$x_{0}'+v_{1}(t-t_{0}')=L+x_{0}+v_{2}(t-t_{0})$，
解得$t=6.5s$。
(3)假设细犬能在匀速阶段追上兔子，则
$[x_{0}'+v_{1}(t'-t_{0}')]^{2}=L^{2}+[x_{0}+v_{2}(t'-t_{0})]^{2}$，
解得$t'=4.5s＞4s$(另一值$t'=0.5s$舍掉)，
可知假设正确，则经4.5s细犬捕获野兔。
答案：
(1)$28m$
(2)$6.5s$
(3)$4.5s$