2025年点金训练精讲巧练高中物理必修第一册教科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年点金训练精讲巧练高中物理必修第一册教科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
任务二 追及相遇问题
活动$1$ 假设资料$2$驾驶员的正常反应时间为$0.3\sim0.8\ s$,刹车时机动车的加速度一般为$5.0\sim8.0\ m/s^2$。结合以上数据,请通过计算来说明车速为每小时$100\ km$时,安全距离为$100\ m$的理论依据。
活动$1$ 假设资料$2$驾驶员的正常反应时间为$0.3\sim0.8\ s$,刹车时机动车的加速度一般为$5.0\sim8.0\ m/s^2$。结合以上数据,请通过计算来说明车速为每小时$100\ km$时,安全距离为$100\ m$的理论依据。
答案:
活动1 提示:汽车速度$v_{0}=100km/h\approx27.8m/s$,
当驾驶员反应时间$t_{0}=0.8s$,刹车加速度$a=5.0m/s^{2}$时,
刹车距离最长,此时驾驶员反应时间内汽车做匀速直线运动,满足如下关系:
$x_{1}=v_{0}t=27.8×0.8m=22.24m$,
反应时间过后汽车开始做匀减速直线运动,满足如下关系:
$v^{2}-v_{0}^{2}=2ax_{2}$,
由于$v=0$,代入数据解得$x_{2}\approx77.28m$,
故驾驶员从反应刹车到停止运动的位移为
$x=x_{1}+x_{2}=99.52m$,
故车速超过每小时$100km$时容易发生追尾事故,应当与同车道前车保持$100m$以上的距离。
当驾驶员反应时间$t_{0}=0.8s$,刹车加速度$a=5.0m/s^{2}$时,
刹车距离最长,此时驾驶员反应时间内汽车做匀速直线运动,满足如下关系:
$x_{1}=v_{0}t=27.8×0.8m=22.24m$,
反应时间过后汽车开始做匀减速直线运动,满足如下关系:
$v^{2}-v_{0}^{2}=2ax_{2}$,
由于$v=0$,代入数据解得$x_{2}\approx77.28m$,
故驾驶员从反应刹车到停止运动的位移为
$x=x_{1}+x_{2}=99.52m$,
故车速超过每小时$100km$时容易发生追尾事故,应当与同车道前车保持$100m$以上的距离。
活动$2$ 假设在直线公路上$A$车以$v_A = 30\ m/s$的速度匀速行驶,因大雾天气能见度低,当司机发现正前方有一辆同向匀速运动的$B$车时,两车距离仅有$x_0 = 92\ m$,此时$B$车的速度$v_B = 10\ m/s$,$A$车司机立即刹车(不计反应时间)做匀减速直线运动,加速度大小为$2\ m/s^2$(两车均视为质点),通过计算判断$A$能否撞上$B$车。若能,求$A$车从刹车开始到撞上$B$车的时间(假设$B$车一直匀速运动)。
答案:
活动2 提示:设两车速度相等,所需的时间为$t_{0}$,则
$v_{A}-a_{A}t_{0}=v_{B}$,
解得$t_{0}=10s$,
此时A车的位移$x_{A}=v_{A}t_{0}-\frac{1}{2}a_{A}t_{0}^{2}=200m$,
B车的位移$x_{B}=v_{B}t_{0}=100m$,
因为$x_{A}>x_{B}+92m$,故A车会撞上B车。设撞上B车的时间为$t_{1}$,则有$v_{A}t_{1}-\frac{1}{2}a_{A}t_{1}^{2}=92m+v_{B}t_{1}$,
解得$t_{1}=(10+2\sqrt{2})s$(舍去)或$t_{1}=(10-2\sqrt{2})s$,
故时间为$t_{1}=(10-2\sqrt{2})s$。
$v_{A}-a_{A}t_{0}=v_{B}$,
解得$t_{0}=10s$,
此时A车的位移$x_{A}=v_{A}t_{0}-\frac{1}{2}a_{A}t_{0}^{2}=200m$,
B车的位移$x_{B}=v_{B}t_{0}=100m$,
因为$x_{A}>x_{B}+92m$,故A车会撞上B车。设撞上B车的时间为$t_{1}$,则有$v_{A}t_{1}-\frac{1}{2}a_{A}t_{1}^{2}=92m+v_{B}t_{1}$,
解得$t_{1}=(10+2\sqrt{2})s$(舍去)或$t_{1}=(10-2\sqrt{2})s$,
故时间为$t_{1}=(10-2\sqrt{2})s$。
任务三 位移差公式的理解及应用
活动1 在测量小车的加速度的实验中,让小车由静止开始做匀加速直线运动,打点计时器的打点周期为T,打出的纸带如图所示,0、1、2、3是纸带上的前4个点。
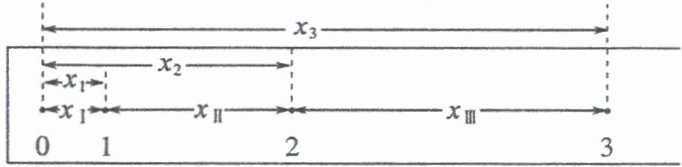
设初速度为$v_0,$则前1T内、2T内、3T内$\cdots\cdots$的位移分别为
$x_1 = v_0T + \frac{1}{2}aT^2$
$x_2 = v_0 \cdot 2T + \frac{4}{2}aT^2$
$x_3 = v_0 \cdot 3T + \frac{9}{2}aT^2$
$\cdots\cdots$
所以第一个T内、第二个T内、第三个T内$\cdots\cdots$的位移分别为
$x_1 = x_1 = $
$x_III = x_3 - x_2 = $
活动1 在测量小车的加速度的实验中,让小车由静止开始做匀加速直线运动,打点计时器的打点周期为T,打出的纸带如图所示,0、1、2、3是纸带上的前4个点。

设初速度为$v_0,$则前1T内、2T内、3T内$\cdots\cdots$的位移分别为
$x_1 = v_0T + \frac{1}{2}aT^2$
$x_2 = v_0 \cdot 2T + \frac{4}{2}aT^2$
$x_3 = v_0 \cdot 3T + \frac{9}{2}aT^2$
$\cdots\cdots$
所以第一个T内、第二个T内、第三个T内$\cdots\cdots$的位移分别为
$x_1 = x_1 = $
$v_{0}T+\frac{1}{2}aT^{2}$
$x_II = x_2 - x_1 = $$v_{0}T+\frac{3}{2}aT^{2}$
$x_III = x_3 - x_2 = $
$v_{0}T+\frac{5}{2}aT^{2}$
$\cdots\cdots$则有$x_II - x_1 = $$aT^{2}$
,x_III - x_II = $aT^{2}$
$\cdots\cdots$所以$\Delta x = x_II - x_1 = x_III - x_II = \cdots = $$aT^{2}$
答案:
活动1 $v_{0}T+\frac{1}{2}aT^{2}$ $v_{0}T+\frac{3}{2}aT^{2}$ $v_{0}T+\frac{5}{2}aT^{2}$ $aT^{2}$ $aT^{2}$ $aT^{2}$
。活动2 如图所示是某同学测量做直线运动的物体的瞬时速度时得到的一条纸带(实验中交流电源的频率为50\ Hz),依照打点的先后顺序取计数点1、2、3、4、5、6、7,相邻两计数点间还有4个点未画出,测得$x_1 = 1.42\ cm,$$x_2 = 1.91\ cm,$$x_3 = 2.40\ cm,$$x_4 = 2.91\ cm,$$x_5 = 3.43\ cm,$$x_6 = 3.92\ cm。$ (1)求打第2个计数点时纸带的速度大小。(2)求小车的加速度大小。
(1)求打第2个计数点时纸带的速度大小。(2)求小车的加速度大小。
 (1)求打第2个计数点时纸带的速度大小。(2)求小车的加速度大小。
(1)求打第2个计数点时纸带的速度大小。(2)求小车的加速度大小。
答案:
活动2 提示:
(1)打第2个计数点时纸带的速度大小为
$v_{2}=\frac{x_{1}+x_{2}}{2T}=\frac{(1.42+1.91)×10^{-2}}{2×0.1}m/s\approx0.17m/s$。
(2)根据$\Delta x=aT^{2}$,得小车的加速度大小为
$a=\frac{x_{4}+x_{5}+x_{6}-x_{1}-x_{2}-x_{3}}{(3T)^{2}}\approx0.50m/s^{2}$。
(1)打第2个计数点时纸带的速度大小为
$v_{2}=\frac{x_{1}+x_{2}}{2T}=\frac{(1.42+1.91)×10^{-2}}{2×0.1}m/s\approx0.17m/s$。
(2)根据$\Delta x=aT^{2}$,得小车的加速度大小为
$a=\frac{x_{4}+x_{5}+x_{6}-x_{1}-x_{2}-x_{3}}{(3T)^{2}}\approx0.50m/s^{2}$。
查看更多完整答案,请扫码查看


