《2025年新课程示径学案作业设计八年级数学上册苏科版》

某人给汽车加油时的计价屏如图所示.已知加油枪流量是 40 L/min,加油前,油箱中有油 6 L.
(1) 在这个过程中有哪些常量、变量？有哪些函数表达式？
(2) 如果每加 1 L 油,需要 8.76 元,那么加油时,金额 y(单位：元)与加油油量 x(单位：L)之间具有函数关系吗？
(3) 在加油过程中,如果用 Q(单位：L)表示油箱中的油量,t(单位：min)表示加油时间,那么 Q 与 t 之间的函数表达式应如何表示？
(4) 由上面的情境,我们得到了两个函数关系,前面我们也得到一些函数表达式,如：$Q = 40-\frac{s}{10}$,$y = 100t$,$g = h - 105$,这些函数表达式有什么共同特点？

答案：
(1)常量：40 L/min，6 L；变量：加油时间t，加油油量x，油箱中的油量Q；函数表达式：x=40t，Q=6+x（或Q=6+40t）。
(2)有函数关系，y=8.76x。
(3)Q=6+40t。
(4)这些函数表达式都是形如y=kx+b（k，b为常数，k≠0）的一次函数（或都是关于自变量的一次整式）。

例 写出下列各个变化过程中两个变量之间的函数表达式,并指出其中的一次函数、正比例函数.
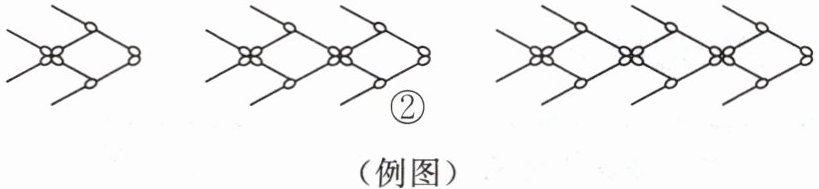
(1) 正方形花圃的周长 C(单位：m)随边长 x(单位：m)的变化而变化.
(2) 正方形花圃的面积 S(单位：$m^{2}$)随边长 x(单位：m)的变化而变化.
(3) 如图①,A,B 两站相距 200 km,若火车从 B 站出发以 320 km/h 的速度驶向 C 站,火车离 A 站的路程 y(单位：km)随行驶时间 t(单位：h)的变化而变化.

(4) 如图②,搭一条“小鱼”需要 8 根火柴棒,每多搭 1 条“小鱼”就要增加 6 根火柴棒.所需火柴棒的根数 S 随着所搭“小鱼”条数 n 的变化而变化.

答案：
(1) $ C = 4x $，是一次函数，也是正比例函数。
(2) $ S = x^2 $，不是一次函数，也不是正比例函数。
(3) $ y = 320t + 200 $（$ t \geq 0 $），是一次函数，不是正比例函数。
(4) $ S = 6n + 2 $（$ n $为正整数），是一次函数，不是正比例函数。