《2025年新课程示径学案作业设计八年级数学上册苏科版》

1. 如图,用纸板挡住两个三角形的一部分,你能画出这两个三角形吗？如果能,你画的三角形和其他同学画的三角形能够完全重合吗？

答案： 本题可根据全等三角形的判定定理“角边角”（ASA）来判断能否画出三角形以及所画三角形是否完全重合。
两个三角形均有两个角及它们的夹边露出，根据“角边角”判定定理可知：
能否画出这两个三角形：可以画出这两个三角形。因为已知两个角以及它们的夹边，根据三角形内角和为$180^{\circ}$，可求出第三个角，再结合已知的夹边，就能确定三角形的形状和大小，所以能够画出这两个三角形。
所画三角形是否完全重合：能够完全重合。由于这两个三角形满足“角边角”的条件，根据全等三角形的判定定理“角边角”（ASA），满足该条件的两个三角形全等，全等三角形能够完全重合。
综上，答案为能画出这两个三角形，且画的三角形和其他同学画的三角形能够完全重合。

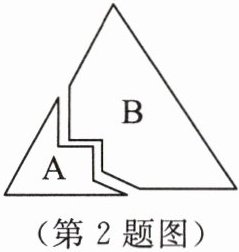
2. 如图,小明踢球时不慎把一块三角形玻璃打碎为 A,B 两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢？如果可以,带哪块去合适呢？为什么？

答案： 可以只带其中一块碎片去商店，带B块去合适。
理由：带A块去，只有两个角，不能确定三角形的大小和形状（AAA不能判定三角形全等）；带B块去，有两个角以及它们的夹边，根据“角边角”（ASA）判定定理，可以确定与原来一样的三角形玻璃。

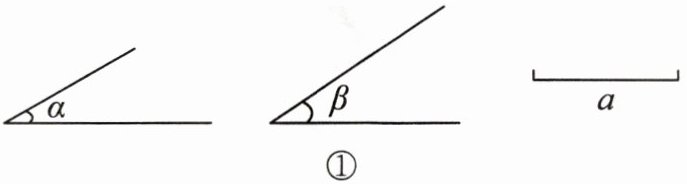
例 如图①,请用尺和圆规画一个△ABC,使得∠A = α,∠B = β,AB = a。将你画的三角形和其他同学画的三角形相比较,你有什么发现？

归纳小结：两角及其夹边分别相等的两个三角形全等(简写成角边角或ASA).
几何语言：如图②,在△ABC 和△A'B'C'中,如果
$\left\{ \begin{array} { l } { \angle ______= \angle ______, } \\ { ______= ______, } \\ { \angle ______= \angle ______, } \end{array} \right.$
那么△ABC ______ △A'B'C'( ).

答案： 两角及其夹边分别相等；角边角；ASA；A；A'；AB；A'B'；B；B'；≌；ASA